题目内容
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.

(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究 轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.

(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)探究
 轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,直接写出点P的坐标;若不存在,请说明理由.(1)y = x2-2x-3, D的坐标为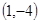 (2)是直角三角形,理由见解析(3)P1(0,0),P2(9,0)
(2)是直角三角形,理由见解析(3)P1(0,0),P2(9,0)
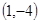 (2)是直角三角形,理由见解析(3)P1(0,0),P2(9,0)
(2)是直角三角形,理由见解析(3)P1(0,0),P2(9,0)解:(1)设该抛物线的解析式为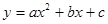 ,
,
由抛物线与y轴交于点C(0,-3),可知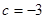 . (1分)
. (1分)
即抛物线的解析式为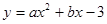 .
.
把A(-1,0)、B(3,0)代入, 得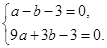
解得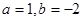 .(3分)∴ 抛物线的解析式为y = x2-2x-3.
.(3分)∴ 抛物线的解析式为y = x2-2x-3.
∴ 顶点D的坐标为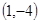 (4分).(设为交点式参照给分)
(4分).(设为交点式参照给分)
(2)以B、C、D为顶点的三角形是直角三角形. (5分)理由如下:
过点D分别作 轴、
轴、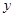 轴的垂线,垂足分别为E、F.
轴的垂线,垂足分别为E、F.
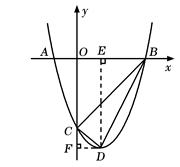
在Rt△BOC中,OB=3,OC=3,
∴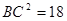 .在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,
.在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,
∴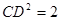 .在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,
.在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,
∴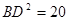 .
.
∴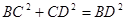 , 故△BCD为直角三角形.(7分)
, 故△BCD为直角三角形.(7分)
(3)符合条件的点有二个:P1(0,0),P2(9,0).
(1)利用待定系数法将A(-1,0)、B(3,0),C(0,-3),代入y=ax2+bx+c,求出二次函数解析式即可;利用配方法直接求出顶点坐标即可;
(2)过点D分别作 轴、
轴、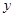 轴的垂线,垂足分别为E、F;根据勾股定理的逆定理进行解答
轴的垂线,垂足分别为E、F;根据勾股定理的逆定理进行解答
(3)根据相似三角形的判定方法分别得出即可
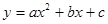 ,
,由抛物线与y轴交于点C(0,-3),可知
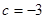 . (1分)
. (1分)即抛物线的解析式为
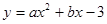 .
. 把A(-1,0)、B(3,0)代入, 得
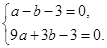
解得
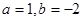 .(3分)∴ 抛物线的解析式为y = x2-2x-3.
.(3分)∴ 抛物线的解析式为y = x2-2x-3. ∴ 顶点D的坐标为
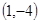 (4分).(设为交点式参照给分)
(4分).(设为交点式参照给分)(2)以B、C、D为顶点的三角形是直角三角形. (5分)理由如下:
过点D分别作
 轴、
轴、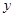 轴的垂线,垂足分别为E、F.
轴的垂线,垂足分别为E、F.
在Rt△BOC中,OB=3,OC=3,
∴
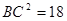 .在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,
.在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,∴
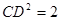 .在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,
.在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,∴
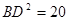 .
. ∴
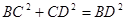 , 故△BCD为直角三角形.(7分)
, 故△BCD为直角三角形.(7分) (3)符合条件的点有二个:P1(0,0),P2(9,0).
(1)利用待定系数法将A(-1,0)、B(3,0),C(0,-3),代入y=ax2+bx+c,求出二次函数解析式即可;利用配方法直接求出顶点坐标即可;
(2)过点D分别作
 轴、
轴、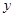 轴的垂线,垂足分别为E、F;根据勾股定理的逆定理进行解答
轴的垂线,垂足分别为E、F;根据勾股定理的逆定理进行解答(3)根据相似三角形的判定方法分别得出即可

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 与
与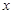 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当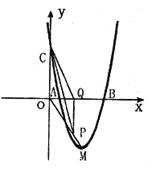

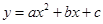 图象的一部分,图象过
图象的一部分,图象过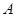 点(3,0),二次函数图象对称轴为
点(3,0),二次函数图象对称轴为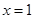 ,给出四个结论:①
,给出四个结论:①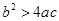 ;②
;②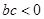 ;③
;③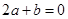 ;④
;④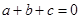 ,其中正确结论是( )
,其中正确结论是( )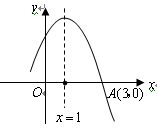
 厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为
厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为 和
和 .
. 
 的顶点坐标为 ( )
的顶点坐标为 ( )