Question

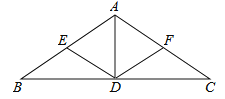
【题目】（本题满分7分）如图，在△ABC中，AB＝AC，点E，F分别是边AB，AC的中点，点D在边BC上．若DE＝DF，AD＝2，BC＝6，求四边形AEDF的周长．

Answer 1

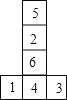
【答案】．

【解析】

试题分析：先由SSS证明△ADE≌△ADF，得出∠DAE=∠DAF，即AD平分∠BAC，再由等腰三角形的三线合一性质得出BD=CD=BC=3，AD⊥BC，根据勾股定理求出AB，由直角三角形斜边上的中线性质得出DE=AB，DF=AC，证出AE=AF=DE=DF，即可求出结果．

试题解析：∵点E，F分别是边AB，AC的中点，∴AE=BE=AB，AF=CF=AC，∵AB=AC，∴AE=AF，在△ADE和△ADF中，∵AE=AF，DE=DF，AD=AD，∴△ADE≌△ADF（SSS），∴∠DAE=∠DAF，即AD平分∠BAC，∴BD=CD=BC=3，AD⊥BC，∴∠ADB=∠ADC=90°，∴AB===，∵在Rt△ABD和Rt△ACD中，E，F分别是边AB，AC的中点，∴DE=AB，DF=AC，∴AE=AF=DE=DF，∴四边形AEDF的周长=4AE=2AB=．