题目内容
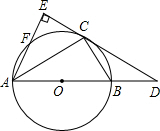 已知:如图,AB是半圆O的直径,D是AB延长线上的一点,AE⊥DC,交DC的延长线于点E,交半圆O于点F,且C为
已知:如图,AB是半圆O的直径,D是AB延长线上的一点,AE⊥DC,交DC的延长线于点E,交半圆O于点F,且C为 | BF |
(1)求证:DE是半圆O的切线;
(2)请说明∠EAC=∠BCD的理由.
分析:(1)连接BF,OC,根据C是
的中点可以得到OC⊥BF,根据直径所对的圆周角是直角可以得到BF⊥AE,则BF∥CE,因而可以证得OC⊥DE,从而证得DE是半圆O的切线;
(2)根据AB是半圆O的直径,∠ACB=90°,则∠ACE+∠BCD=90°,在直角△ACE中,∠ACE+∠EAC=90°,即可得到∠EAC=∠BCD.
 |
| BF |
(2)根据AB是半圆O的直径,∠ACB=90°,则∠ACE+∠BCD=90°,在直角△ACE中,∠ACE+∠EAC=90°,即可得到∠EAC=∠BCD.
解答: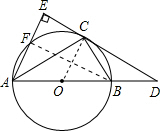 证明:(1)连接BF,OC.
证明:(1)连接BF,OC.
∵C为
的中点,
∴OC⊥BF,
又∵AB是半圆O的直径,
∴BF⊥AE,
∴BF∥CE,
∴OC⊥DE,
∴DE是半圆O的切线;
(2)∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠ACE+∠BCD=90°,
又∵直角△ACE中,∠ACE+∠EAC=90°,
∴∠EAC=∠BCD.
 证明:(1)连接BF,OC.
证明:(1)连接BF,OC.∵C为
 |
| BF |
∴OC⊥BF,
又∵AB是半圆O的直径,
∴BF⊥AE,
∴BF∥CE,
∴OC⊥DE,
∴DE是半圆O的切线;
(2)∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠ACE+∠BCD=90°,
又∵直角△ACE中,∠ACE+∠EAC=90°,
∴∠EAC=∠BCD.
点评:本题考查了圆周角定理,以及切线的判定,判定切线的问题常用的方法是转化成证明垂直问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
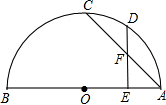 已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.①
已知:如图,AB为⊙O的直径,C、D是半圆弧上的两点,E是AB上除O外的一点,AC与DE相交于F.① =-
=- ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.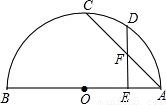
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.