题目内容
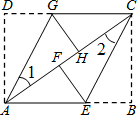 如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.求证:四边形AECG是平行四边形.
如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.求证:四边形AECG是平行四边形.分析:由四边形ABCD是矩形,可得AD∥BC,AB∥CD,又由平行线的性质,可得∠DAC=∠BCA,然后根据折叠的性质可得:∠1=
∠DAC,∠2=
∠BCA,即可证得AG∥CE,根据有两组对边分别平行的四边形是平行四边形,即可证得四边形AECG是平行四边形.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵四边形ABCD是矩形,
∴AD∥BC,AB∥CD,
∴∠DAC=∠BCA,
由折叠的性质可得:∠1=
∠DAC,∠2=
∠BCA,
∴∠1=∠2,
∴AG∥CE,
∴四边形AECG是平行四边形.
∴AD∥BC,AB∥CD,
∴∠DAC=∠BCA,
由折叠的性质可得:∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2,
∴AG∥CE,
∴四边形AECG是平行四边形.
点评:此题考查了折叠的性质、矩形的性质、以及平行四边形的判定.此题难度不大,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
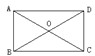 7、如图,ABCD是矩形,对角线AC、BD交于点O,要找出图中的全等三角形,最多可找出( )对?
7、如图,ABCD是矩形,对角线AC、BD交于点O,要找出图中的全等三角形,最多可找出( )对?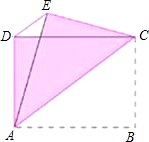 如图,ABCD是矩形,AB=4cm,AD=3cm,把矩形沿直线AC折叠.点B落在E处,连接DE.四边形ACED是什么图形?为什么?它的面积是多少?周长呢?
如图,ABCD是矩形,AB=4cm,AD=3cm,把矩形沿直线AC折叠.点B落在E处,连接DE.四边形ACED是什么图形?为什么?它的面积是多少?周长呢?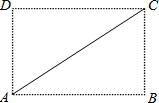 如图,ABCD是矩形纸片,翻折∠B、∠D使BC边、AD边恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
如图,ABCD是矩形纸片,翻折∠B、∠D使BC边、AD边恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.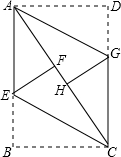 (2009•郑州模拟)如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(2009•郑州模拟)如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.