题目内容
【题目】将矩形纸片ABCD按如图方式折叠,使点D与点B重合,点C落到C′处,折痕为EF.若AD=9AB=6,求折痕EF的长.
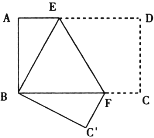
【答案】折痕EF长为![]()
【解析】
由矩形的性质和折叠的性质得BE=DE,∠A=90°,∠BEF=∠DEF,AD∥BC;根据AD∥BCd得到∠BFE=∠BEF,说明BF=BE;在 Rt△ABE 中,设 AE=x,则 BE=DE=9-x. 由勾股定理和线段的和差即可解答。
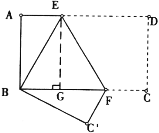
解:依题意,得:BE=DE,∠A=90°,∠BEF=∠DEF.
∵AD∥BC,
∴∠DEF=∠BFE.
∴∠BFE=∠BEF.
∴BF=BE.
在 Rt△ABE 中,设 AE=x,则 BE=DE=9-x. 由勾股定理,得 x2+62=(9-x)2
∴ x ![]() ,即 AE
,即 AE ![]() .
.
∴BE=BF=DE=AD-AE=![]()
过 E 点作 EG⊥BF 于 G 点,则得矩形 ABGE.
EG=AB=6,BG=AE=![]()
∴FG=BF-BG= ![]()
![]() 4 .
4 .
EF ![]()
即折痕 EF 长为![]()

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目