题目内容
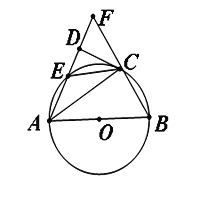
【题目】如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线,
(1)求证:直线CD是⊙O的切线.
(2)求证:△FEC是等腰三角形
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)先判断出∠FAC=∠ACO,进而得出AF∥CO,即可得出结论;
(2)先用等腰三角形的三线合一得出AF=AB.再用同角的补角相等得出∠FEC=∠B 即可得出结论.
试题解析:(1)连接OC,则∠CAO=∠ACO,
又∠FAC=∠CAO
∴∠FAC=∠ACO,
∴AF∥CO,
而CD⊥AF,
∴CO⊥CD,
即直线CD是⊙O的切线;
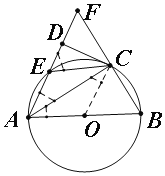
(2)∵AB是⊙O的直径,
∴∠ACB=90°
又∠FAC=∠CAO
∴AF=AB(三线合一),
∴∠F=∠B,
∵四边形EABC是⊙O的内接四边形,
∵∠FEC+∠AEC=180°,∠B+∠AEC=180°
∴∠FEC=∠B
∴∠F=∠FEC,
即EC=FC
所以△FEC是等腰三角形.

练习册系列答案
相关题目

