题目内容
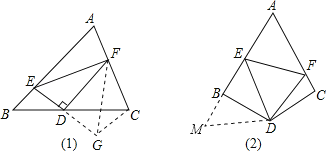
【题目】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.

①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
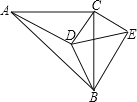
(2)如图(2),在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
【答案】(1)①见解析;②BE2+CF2=EF2.证明见解析;(2)EF= EB+CF,证明见解析.
【解析】
试题分析:(1)①如图(1)延长ED到G,使DG=ED,连接CG,FG,根据条件证明△DCG≌△DBE,得DG=DE,CG=BE,易证FD垂直平分线段EG,则FG=FE,把问题转化到△CFG中,运用三边关系比较大小;
②结论:BE2+CF2=EF2.若∠A=90°,则∠B+∠C=90°,可证∠FCG=∠FCD+∠DCG=∠FCD+∠B=90°,在Rt△CFG中,由勾股定理探索线段BE、CF、EF之间的数量关系;
(2)如图(2),结论:EF=EB+FC.延长AB到M,使BM=CF,根据条件证明△BDM≌△CDF,则DM=DF,再证明△DEM≌△DEF,从而得EF=EM=EB+BM=EB+CF.
(1)①证明:如图(1)延长ED到G,使DG=ED,连接CG,FG,
∵在△DCG与△DBE中,
 ,
,
∴△DCG≌△DBE(SAS),
∴DG=DE,CG=BE,
又∵DE⊥DF,
∴FD垂直平分线段EG,
∴FG=FE,
在△CFG中,CG+CF>FG,即BE+CF>EF;
②结论:BE2+CF2=EF2.
理由:∵∠A=90°,
∴∠B+∠ACD=90°,
由①∠FCG=∠FCD+∠DCG=∠FCD+∠B=90°,
∴在Rt△CFG中,由勾股定理,得CG2+CF2=FG2,
即BE2+CF2=EF2;
(2)如图(2),结论:EF=EB+FC.
理由:延长AB到M,使BM=CF,
∵∠ABD+∠C=180°,又∠ABD+∠MBD=180°,
∴∠MBD=∠C,而BD=CD,
∴△BDM≌△CDF,
∴DM=DF,∠BDM=∠CDF,
∴∠EDM=∠EDB+∠BDM=∠EDB+∠CDF=∠CDB﹣∠EDF=120°﹣60°=60°=∠EDF,
∴△DEM≌△DEF,
∴EF=EM=EB+BM=EB+CF.