Question

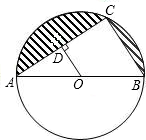如图，已知AB是⊙O的直径，点C在⊙O上，且AB=13，BC=5．
（1）求sin∠BAC的值；
（2）如果OD⊥AC，垂足为D，求AD的长；
（3）求图中阴影部分的面积．（精确到0.1）

Answer 1

分析：（1）已知AB是⊙O的直径，则∠ACB=90°，在直角△ABC中根据勾股定理，求出BC，即可得到sin∠BAC的值．
（2）OD⊥AC，则满足垂径定理，因而在直角△ABC中，根据勾股定理就可以求出AD的长．
（3）阴影部分的面积就是半圆的面积减去直角△ABC的面积．

解答：解：（1）∵AB是⊙O的直径，点C在⊙O上，
∴∠ACB=90°．
∵AB=13，BC=5，
∴sin∠BAC=

BC

AB

=

5

13

；

（2）在Rt△ABC中，
AC=

AB2-BC2

=

132-52

=12，
∴AD=

1

2

AC=6；

（3）S_阴影部分=

1

2

π×(

13

2

)2-

1

2

×5×12≈36.3（平方单位）．

点评：阴影部分的面积可以看作是半圆的面积减去直角三角形的面积．求不规则的图形的面积，可以转化为几个规则图形的面积的和或差来求．