题目内容
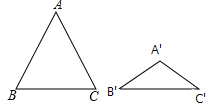
【题目】如图，△ABC与△A′B′C′都是等腰三角形，且AB=AC=5，A′B′=A′C′=3，若∠B+∠B′=90°，则△ABC与△A′B′C′的面积比为（ ）
A．25：9 B．5：3 C．
：
D．5
：3
【答案】A．
【解析】
试题分析：过A 作AD⊥BC于D，过A′作A′D′⊥B′C′于D′，∵△ABC与△A′B′C′都是等腰三角形，∴∠B=∠C，∠B′=∠C′，BC=2BD，B′C′=2B′D′，∴AD=ABsinB，A′D′=A′B′sinB′，BC=2BD=2ABcosB，B′C′=2B′D′=2A′B′cosB′，∵∠B+∠B′=90°，∴sinB=cosB′，sinB′=cosB，∵S△BAC=
ADBC=ABsinB2ABcosB=25sinBcosB，S△A′B′C′=A′D′B′C′=A′B′cosB′2A′B′sinB′=9sinB′cosB′，∴S△BAC：S△A′B′C′=25：9．故选A．
练习册系列答案
优加精卷系列答案
相关题目
