题目内容
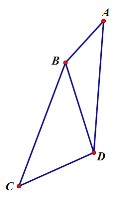
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 于点
于点![]() ,连
,连![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ..其中正确结论的个数为( )
..其中正确结论的个数为( )

A. 5 B. 4 C. 3 D. 2
【答案】B
【解析】①由等边三角形与等腰直角三角形知△CAD是等腰三角形且顶角∠CAD=150°,据此可判断;②求出∠AFP和∠FAG度数,从而得出∠AGF度数,据此可判断;③证△ADF≌△BAH即可判断;④由∠AFG=∠CBG=60°、∠AGF=∠CGB即可得证;⑤设PF=x,则AF=2x、AP=![]() x,设EF=a,由△ADF≌△BAH知BH=AF=2x,根据△ABE是等腰直角三角形之BE=AE=a+2x,据此得出EH=a,证△PAF∽△EAH得
x,设EF=a,由△ADF≌△BAH知BH=AF=2x,根据△ABE是等腰直角三角形之BE=AE=a+2x,据此得出EH=a,证△PAF∽△EAH得![]() ,从而得出a与x的关系即可判断.
,从而得出a与x的关系即可判断.
∵△ABC为等边三角形,△ABD为等腰直角三角形,
∴∠BAC=60°、∠BAD=90°、AC=AB=AD,∠ADB=∠ABD=45°,
∴△CAD是等腰三角形,且顶角∠CAD=150°,
∴∠ADC=15°,故①正确;
∵AE⊥BD,即∠AED=90°,
∴∠DAE=45°,
∴∠AFG=∠ADC+∠DAE=60°,∠FAG=45°,
∴∠AGF=75°,
由∠AFG≠∠AGF知AF≠AG,故②错误;
记AH与CD的交点为P,
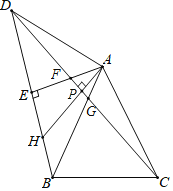
由AH⊥CD且∠AFG=60°知∠FAP=30°,
则∠BAH=∠ADC=15°,
在△ADF和△BAH中,
∵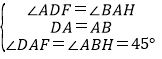 ,
,
∴△ADF≌△BAH(ASA),
∴DF=AH,故③正确;
∵∠AFG=∠CBG=60°,∠AGF=∠CGB,
∴△AFG∽△CBG,故④正确;
在Rt△APF中,设PF=x,则AF=2x、AP=![]() x,
x,
设EF=a,
∵△ADF≌△BAH,
∴BH=AF=2x,
△ABE中,∵∠AEB=90°、∠ABE=45°,
∴BE=AE=AF+EF=a+2x,
∴EH=BE-BH=a+2x-2x=a,
∵∠APF=∠AEH=90°,∠FAP=∠HAE,
∴△PAF∽△EAH,
∴![]() ,即
,即![]() ,
,
整理,得:2x2=(![]() -1)ax,
-1)ax,
由x≠0得2x=(![]() -1)a,即AF=(
-1)a,即AF=(![]() -1)EF,故⑤正确;
-1)EF,故⑤正确;
故选:B.

【题目】小华根据学习函数的经验,对函数![]() 的图象与性质进行了研究,下面是小华的研究过程,请补充完成.
的图象与性质进行了研究,下面是小华的研究过程,请补充完成.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
| 4 | 5 |
|
|
| m | 2 | 1 | 0 | n | 2 | 3 |
|
其中,m= ,n= ;
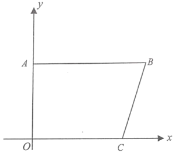
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出该函数的图象;

(3)观察图象,写出该函数的两条性质;
(4)进一步研究函数图象发现:
①方程![]() 有 个实数根;
有 个实数根;
②不等式![]() 的解集为 .
的解集为 .