题目内容
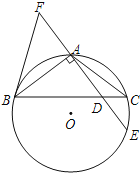
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与![]() 轴交于点C,顶点为D,对称轴与
轴交于点C,顶点为D,对称轴与![]() 轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交
轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交![]() 轴交于点G.
轴交于点G.
(1)如图①,求直线CE的解析式和顶点D的坐标;
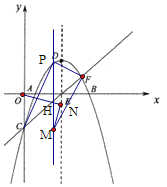
(2)如图①,点P为直线CF上方抛物线上一点,连接PC、PF,当△PCF的面积最大时,点M是过P垂直于![]() 轴的直线l上一点,点N是抛物线对称轴上一点,求
轴的直线l上一点,点N是抛物线对称轴上一点,求![]() 的最小值;
的最小值;
(3)如图②,过点D作![]() 交
交![]() 轴于点I,将△GDI沿射线GB方向平移至
轴于点I,将△GDI沿射线GB方向平移至![]() 处,将
处,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,当旋转到一定度数时,点
,当旋转到一定度数时,点![]() 会与点I重合,记旋转过程中的
会与点I重合,记旋转过程中的![]() 为
为![]() ,若在整个旋转过程中,直线G’’I’’分别交x轴和直线GD’于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.
,若在整个旋转过程中,直线G’’I’’分别交x轴和直线GD’于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.



【答案】(1)![]() D
D![]()
(2)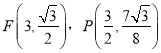 最小值为
最小值为![]()
(3)略
【解析】(1)根据二次函数解析式![]() 得:与y轴的额交点坐标为(0,-
得:与y轴的额交点坐标为(0,-![]() ),对称轴为直线x=2,则E(2,0),D
),对称轴为直线x=2,则E(2,0),D![]() 设直线CE :
设直线CE : ![]() 根据两点坐标,列方程组
根据两点坐标,列方程组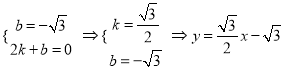 .
.
(2)联立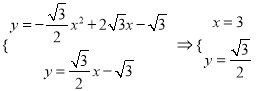 ,即
,即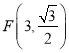 ,作PH垂直x轴,较x轴于H,设P
,作PH垂直x轴,较x轴于H,设P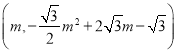 H(m,
H(m, ![]() ),则PH=
),则PH= ![]() ,则S=
,则S=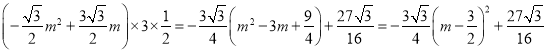 ,得当m=
,得当m=![]() 时,面积最大,当
时,面积最大,当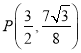
![]() 的最小值为
的最小值为![]() .
.
(3)不存在.

练习册系列答案
相关题目
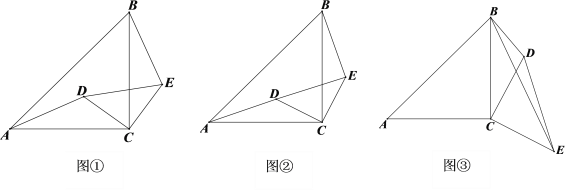
【题目】如图1至图3是将正方体截去一部分后得到的几何体.

(1)根据要求填写表格:
面数/f | 顶点数/v | 棱数/e | |
图1 | _____ | _____ | ____ |
图2 | _____ | _____ | _____ |
图3 | ___ | _____ | ____ |
(2)猜想f,v,e三个数量间的关系.
(3)根据猜想计算,若一个几何体的顶点有2 019个,棱有4 035条,试求出它的面数.