Question

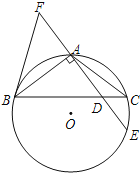
【题目】如图，在△ABC中，AB=AC，⊙O是△ABC的外接圆，AE⊥AB交BC于点D，交⊙O于点E，F在DA的延长线上，且AF=AD．若AF=3，tan∠ABD=，求⊙O的直径．

Answer 1

【答案】

【解析】试题分析：如图，连接BE．利用等腰三角形“三线合一”的性质得到BF=BD；然后根据圆周角定理推知∠FBA=∠ABC=∠C=∠E，BE是⊙O的直径．利用锐角三角函数的定义可以来求BE的长度．

试题解析：

如图，连接BE．

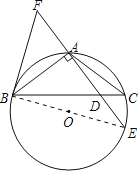
∵AF=AD，AB⊥EF，

∴BF=BD．是直径

∵AB=AC，

∴∠FBA=∠ABC=∠C=∠E．

∵tan∠ABD=，

∴tanE=tan∠FBA=．

在Rt△ABF中，∠BAF=90°．

∵tan∠FBA== ，AF=3，

∴AB=4．

∵∠BAE=90°，

∴BE是⊙O的直径．

∵tanE=tan∠FBA= ，AB=4，

∴设AB=3x，AE=4x，

∴BE=5x，

∵3x=4，

∴BE=5x=，

即⊙O的直径是．