题目内容
若x2+y2+ =2x+y,那么xy+yx=________.
=2x+y,那么xy+yx=________.

分析:首先将原式移项配方,可得:∴(x-1)2+(y-
 )2=0,由非负数的和为零,则每个为零的性质,即可求得x与y的值,则问题得解.
)2=0,由非负数的和为零,则每个为零的性质,即可求得x与y的值,则问题得解.解答:∵x2+y2+
 =2x+y,
=2x+y,∴x2+y2+
 -2x-y=0,
-2x-y=0,∴(x-1)2+(y-
 )2=0,
)2=0,∴x-1=0,y-
 =0,
=0,∴x=1,y=
 ,
,∴xy+yx=1+
 =
= .
.故答案为:
 .
.点评:此题考查了配方法与非负数的和为零,则每个为零的性质.解题的关键是要注意分析.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
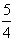 =2x+y,那么xy+yx=( )。
=2x+y,那么xy+yx=( )。