题目内容
【题目】如图,已知等腰△ABC,AC=BC=10.AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
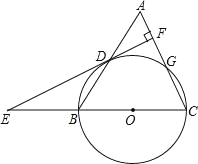
(1)求证:直线EF是⊙O的切线;
(2)求DF的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)求证直线EF是⊙O的切线,只要连接OD证明OD⊥EF即可;
(2)由BC是⊙O直径,得到CD⊥AB,在Rt△ACD中,由勾股定理得:CD=![]() =8,由于EF⊥AC,CD⊥AB,得出∠AFD=∠CDB=90°,推出△ADF∽△BCD,得到比例式,即可得到结论.
=8,由于EF⊥AC,CD⊥AB,得出∠AFD=∠CDB=90°,推出△ADF∽△BCD,得到比例式,即可得到结论.
试题解析:(1)连接CD,OD,
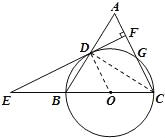
∵AC=BC,
∴∠A=∠ABC,
∵OD=OB,
∴∠ABC=∠BDO,
∴∠A=∠BDO,
∴OD∥AC,
∵EF⊥AC,
∴EF⊥OD,
∵OD为半径,
∴EF是⊙O的切线;
(2)∵BC是⊙O直径,
∴CD⊥AB,
∵AC=BC=10,又AB=12,
∴AD=BD=6,
在Rt△ACD中,由勾股定理得:CD=![]() =8,
=8,
∵EF⊥AC,CD⊥AB,
∴∠AFD=∠CDB=90°,
又∵∠A=∠CBD,
∴△ADF∽△BCD,
∴![]() ,
,
∴![]() ,即DF=
,即DF=![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
