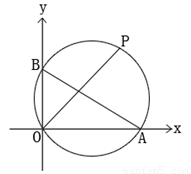
题目内容
如下图,已知 、
、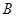 两点的坐标分别是(
两点的坐标分别是( ,0)(0,2),
,0)(0,2),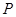 是△
是△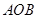 外接圆上的一点,且∠
外接圆上的一点,且∠ =45o,则点
=45o,则点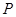 的坐标是 。
的坐标是 。

解析试题分析:由P点在第一象限,∠AOP=45°,可设P(a,a).过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,用含a的代数式分别表示PF,CF,在△CFP中由勾股定理求出a的值,即可求得P点的坐标. ,
,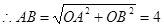 ,
,
∵∠AOP=45°,
P点横纵坐标相等,可设为a.
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(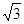 ,1),
,1),
P点在圆上,P点到圆心的距离为圆的半径2.
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,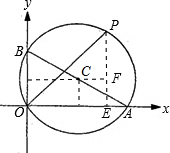
∴∠CFP=90°,
∴PF=a-1,CF=a-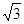 ,PC=2,
,PC=2,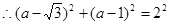 ,舍去不合适的根,
,舍去不合适的根,
可得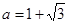 ,
,
则P点坐标为 ,
,
故答案为 。
。
考点:此题主要考查了圆周角定理、勾股定理、等腰直角三角形的判定和性质
点评:解答本题的根据是掌握好圆周角定理:直径所对圆心角是直角。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





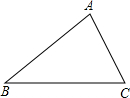 如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)
如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)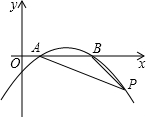 它的横坐标为9,∠PBO=135°,cot∠PAB=
它的横坐标为9,∠PBO=135°,cot∠PAB= 、
、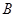 两点的坐标分别是 (
两点的坐标分别是 ( ,0)(0,2),
,0)(0,2),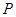 是△
是△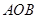 外接圆上的一点,且∠
外接圆上的一点,且∠ =45o,则点
=45o,则点