题目内容
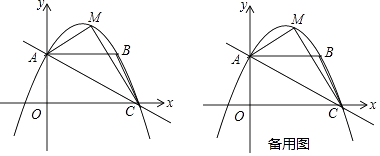
【题目】如图,已知正方形ABCD的边长为2,以DC为底向正方形外作等腰△DEC,连接AE,以AE为腰作等腰△AEF,使得EA=EF,且∠DEC=∠AEF.
(1)求证:△EDC∽△EAF;
(2)求DE·BF的值;
(3)连接CF、AC,当CF⊥AC时,求∠DEC的度数.

【答案】(1)证明见解析;
(2)DE·BF的值为4;
(3)∠DEC的度数为45°.
【解析】(1)先证两对对应角相等得出△EDC∽△EAF;(2)利用(1)的结论推出两边对应成比例且夹角相等得到△BAF∽△DEA,从而求出DE·BF;(3)
解:(1)∵△AEF和△DEC是等腰三角形,且∠DEC=∠AEF,

∴∠EAF=![]()
![]()
∴∠EAF=∠EDC
∴△EDC∽△EAF.
(2)由(1)得△EDC∽△EAF,
∴![]()
∵DC=AB,∴![]()
∵∠DEA=180°-90°-∠EDC-∠DAE=90°-∠EDC-∠DAE,
∠BAF=90°-∠EAF-∠DAE,∴∠BAF=∠DEA
∴△BAF∽△DEA,
∴![]() .即DE·BF=DA·AB=4.
.即DE·BF=DA·AB=4.
(另法:记∠DEC=∠AEF=α,
∴![]() ,
, ![]() ,
,
![]()
∴![]() ,
,
∴![]() )
)

(3)∵DE=CE,AE=FE,∴△ADE≌△FCE
∴AD=FC=BC
∵△BAF∽△DEA,
∴∠ABF=∠EDA , ∴∠FBC=∠CDE
∵△CBF和△EDC是等腰三角形,
∴∠BCF=∠DEC
∵CF⊥AC,∴∠ACF=90°
∵∠ACB=45°,∴∠BCF=45°
∴∠DEC=45°.
“点睛”本题考查相似三角形、等腰三角形的性质、全等三角形的性质、正方形的性质,解题的关键是熟练应用相似三角形性质解决问题,解题时要注意小题间的联系,有一定难度,属于中考压轴题.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案【题目】为了参加市中学生篮球运动后,某校篮球队准备购买10双运动鞋,经统计10双运动鞋的号码(cm)如表所示:
尺码 | 25 | 25.5 | 26 | 26.5 | 27 |
购买量(双) | 2 | 4 | 2 | 1 | 1 |
则这10双运动鞋尺码的众数和中位数分别是( )
A.25.5cm 26cm
B.26cm 25.5cm
C.26cm 26cm
D.25.5cm 25.5cm
【题目】A、B两仓库分别有水泥20吨和30吨,C、D两工地分别需要水泥15吨和35吨.已知从A、B仓库到C、D工地的运价如下表:
到C工地 | 到D工地 | |
A仓库 | 每吨15元 | 每吨12元 |
B仓库 | 每吨10元 | 每吨9元 |
(1)若从A仓库运到C工地的水泥为![]() 吨,则用含x的代数式表示从A仓库运到D工地的水泥为 吨,从B仓库将水泥运到D工地的运输费用为 元;
吨,则用含x的代数式表示从A仓库运到D工地的水泥为 吨,从B仓库将水泥运到D工地的运输费用为 元;
(2)求把全部水泥从A、B两仓库运到C、D两工地的总运输费(用含![]() 的代数式表示并化简);
的代数式表示并化简);
(3)如果从A仓库运到C工地的水泥为15吨时,那么总运输费为多少元?