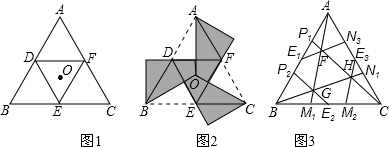
题目内容
阅读下面材料:
镜面对称:镜前的物体与其在镜中的像关于镜面对称
①如果有一个用火柴摆出的等式,而你从镜子中看见的是如下式子:

那么你能立即对这个等式的正确性做出判断吗?
②如图(1),镜前有黑、白两球,如果你用白球瞄准黑球在镜中的像,击出的白球就能经镜面反弹击中黑球.
如果你有两面互相垂直的镜子,你想让击出的白球先后经两个镜面反弹,然后仍能击中黑球,那么你应该怎样瞄准?请仿照图(1)画出图(2)中白球的运动的路线图.
③请利用轴对称解决下面问题:
如图(3)在Rt△ABC中,AB=BC=4cm,E是BC的中点,点P是AC上一动点,则△PBE的周长最小值为

镜面对称:镜前的物体与其在镜中的像关于镜面对称
①如果有一个用火柴摆出的等式,而你从镜子中看见的是如下式子:

那么你能立即对这个等式的正确性做出判断吗?
不正确
不正确
(填“正确”或“不正确”)②如图(1),镜前有黑、白两球,如果你用白球瞄准黑球在镜中的像,击出的白球就能经镜面反弹击中黑球.
如果你有两面互相垂直的镜子,你想让击出的白球先后经两个镜面反弹,然后仍能击中黑球,那么你应该怎样瞄准?请仿照图(1)画出图(2)中白球的运动的路线图.
③请利用轴对称解决下面问题:
如图(3)在Rt△ABC中,AB=BC=4cm,E是BC的中点,点P是AC上一动点,则△PBE的周长最小值为
2
+2
| 5 |
2
+2
cm.(不必写理由)| 5 |

分析:①根据镜面对称原理即可判断答案;
②根据镜面对称就是轴对称关于镜面对称,把物体沿对称轴旋转180°推出即可;
③作B点关于AC的对称点B′点,连接B′E交AC于点P,连接B′C,此时△PBE的周长最小,进而利用勾股定理求出即可.
②根据镜面对称就是轴对称关于镜面对称,把物体沿对称轴旋转180°推出即可;
③作B点关于AC的对称点B′点,连接B′E交AC于点P,连接B′C,此时△PBE的周长最小,进而利用勾股定理求出即可.
解答:解:①实际问题中是:125-50=135,
故不正确;
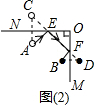
②如图(2)所示:作白球A关于镜面ON的对称点C,作黑球B关于镜面OM的对称点D,连接CD交ON于E,交OM于F,连接AE、BF,
延AE-EF-FB线瞄准,击出的白球先后经两个镜面反弹,仍能击中黑球,
答:延AE-EF-FB线瞄准,击出的白球先后经两个镜面反弹,仍能击中黑球.
 ;
;

③如图(3),作B点关于AC的对称点B′点,连接B′E交AC于点P,
连接B′C,此时△PBE的周长最小,
∵B点关于AC的对称点B′点,
∴BP=B′P,
∵AB=BC=4cm,E是BC的中点,
∴B′C=4cm,EC=2cm,
∴B′E=BP+PE=
=
=2
(cm),
∴△PBE的周长最小值为:(2
+2)cm.
故答案为:2
+2.
故不正确;
②如图(2)所示:作白球A关于镜面ON的对称点C,作黑球B关于镜面OM的对称点D,连接CD交ON于E,交OM于F,连接AE、BF,
延AE-EF-FB线瞄准,击出的白球先后经两个镜面反弹,仍能击中黑球,
答:延AE-EF-FB线瞄准,击出的白球先后经两个镜面反弹,仍能击中黑球.
 ;
;
③如图(3),作B点关于AC的对称点B′点,连接B′E交AC于点P,
连接B′C,此时△PBE的周长最小,
∵B点关于AC的对称点B′点,
∴BP=B′P,
∵AB=BC=4cm,E是BC的中点,
∴B′C=4cm,EC=2cm,
∴B′E=BP+PE=
| EC2+B′C2 |
| 22+42 |
| 5 |
∴△PBE的周长最小值为:(2
| 5 |
故答案为:2
| 5 |
点评:本题主要考查对勾股定理,正方形的性质,轴对称的性质,线段垂直平分线的性质,镜面对称,轴对称-最短路线问题等知识点的理解和掌握,综合运用这些性质进行画图和推理是解此题的关键.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目