题目内容
如图,点A、B在直线l上,AB=24cm,⊙A、⊙B的半径开始都为2cm,⊙A以2cm/s的速度自左向右运动,设运动时间为t(s),
自⊙A开始运动时,⊙B的半径不断增大,其半径r(cm)与时间t之间的关系式为r=2+t.

(1)写出点A、B之间的距离y(cm)与时间t之间的函数关系式;
(2)⊙A出发后多少秒两圆相切?
(3)当t=4时,⊙A停止向右运动,与此同时,⊙B的半径也不再增大,记直线l与⊙B左侧的交点为点C,将⊙A绕点C在平面内旋转360°.问:⊙A与⊙B能否相切?若能,请直接写出相切几次;若不能,请说明理由.
解:(1)当0≤t<12时,y=24-2t;
当t≥12时,y=2t-24.…
(2)①若24-2t=2+t+2,则t= .…
.…
②若24-2t=2+t-2,则t=8.…
③若2t-24=2+t-2,则t=24.…
④若2t-24=2+2+t,则t=28.…
综上可得:当t= 或t=8或t=24或t=28时,两圆相切.…
或t=8或t=24或t=28时,两圆相切.…
(3)相切3次.…
分析:(1)因为⊙A以每秒2厘米的速度自左向右运动,所以此题要分两种情况讨论:
当点A在点B的左侧时,圆心距等于24减去点A所走的路程;
当点A在点B的右侧时,圆心距等于点A走的路程减去24;
(2)在(1)的基础上进行分析,又两圆相切包括内切或外切,所以此题共有4种情况;
(3)分别得出两圆的半径,再根据圆心距得出相切的次数.
点评:考查了圆与圆的位置关系,此题一定要结合图形分析各种不同的情况.注意在解答第二问的时候,⊙B的半径也在不断变化.
当t≥12时,y=2t-24.…
(2)①若24-2t=2+t+2,则t=
 .…
.…②若24-2t=2+t-2,则t=8.…
③若2t-24=2+t-2,则t=24.…
④若2t-24=2+2+t,则t=28.…
综上可得:当t=
 或t=8或t=24或t=28时,两圆相切.…
或t=8或t=24或t=28时,两圆相切.…(3)相切3次.…
分析:(1)因为⊙A以每秒2厘米的速度自左向右运动,所以此题要分两种情况讨论:
当点A在点B的左侧时,圆心距等于24减去点A所走的路程;
当点A在点B的右侧时,圆心距等于点A走的路程减去24;
(2)在(1)的基础上进行分析,又两圆相切包括内切或外切,所以此题共有4种情况;
(3)分别得出两圆的半径,再根据圆心距得出相切的次数.
点评:考查了圆与圆的位置关系,此题一定要结合图形分析各种不同的情况.注意在解答第二问的时候,⊙B的半径也在不断变化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 20、如图,点B、D 在直线MN上.已知∠1=∠2,请你再添上一个条件,使AB∥CD成立.并说明理由.
20、如图,点B、D 在直线MN上.已知∠1=∠2,请你再添上一个条件,使AB∥CD成立.并说明理由.

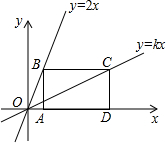 如图,点B,C分别在直线y=2x和直线y=kx上,A,D是x轴上两点,若四边形ABCD是长方形,且AB:AD=1:2,则k的值是( )
如图,点B,C分别在直线y=2x和直线y=kx上,A,D是x轴上两点,若四边形ABCD是长方形,且AB:AD=1:2,则k的值是( )