题目内容
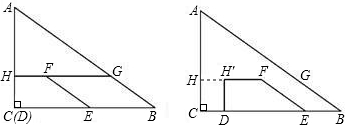
20、如图，点B、D 在直线MN上．已知∠1=∠2，请你再添上一个条件，使AB∥CD成立．并说明理由．（1）你所添的一个条件是：
EB∥FD或EB⊥MN或FD⊥MN（答案不唯一）
；（2）说明你的理由．
分析：（1）此题答案不唯一，只要证得∠ABM=∠CDM即可，根据同位角相等，两直线平行，即可证得AB∥CD；
（2）由EB∥DF，易证得∠ABM=∠CDM，又由同位角相等，两直线平行，即可证得AB∥CD．
（2）由EB∥DF，易证得∠ABM=∠CDM，又由同位角相等，两直线平行，即可证得AB∥CD．
解答：解：（1）故答案为：答案不唯一．如：EB∥FD或EB⊥MN、FD⊥MN．
（2）若EB∥FD．
证明：∵EB∥FD，
∴∠EBM=∠FDM，
∵∠1=∠2，
∴∠ABM=∠CDM，
∴AB∥CD；
若EB⊥MN、FD⊥MN，
证明：∵EB⊥MN、FD⊥MN，
∴∠EBM=∠FDM=90°，
∵∠1=∠2，
∴∠ABM=∠CDM，
∴AB∥CD．
（2）若EB∥FD．
证明：∵EB∥FD，
∴∠EBM=∠FDM，
∵∠1=∠2，
∴∠ABM=∠CDM，
∴AB∥CD；
若EB⊥MN、FD⊥MN，
证明：∵EB⊥MN、FD⊥MN，
∴∠EBM=∠FDM=90°，
∵∠1=∠2，
∴∠ABM=∠CDM，
∴AB∥CD．
点评：此题考查了平行线的性质．注意同位角相等，两直线平行．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
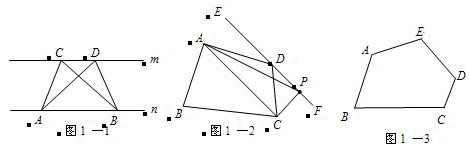
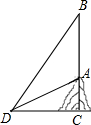（2013•龙湾区一模）如图，热气球从山顶A竖直上升至点B需25秒，点D在地面上，DC⊥AB，垂足为C，从地面上点D分别仰视A，B两点，测得∠ADC=20°，∠BDC=60°，若CD=130米．求该热气球从山顶A竖直上升至点B的平均速度．（结果精确到0.1米/秒）
