题目内容
【题目】已知抛物线过A(－1，0)，B(3，0)两点，与y轴交于C点，且BC=3
，则这条抛物线的解析式为 ( )
A. y=－x2+2x+3 B. y＝x2－2x－3
C. y=x2+2x―3或y＝－x2+2x+3 D. y=－x2+2x+3或y＝x2－2x－3
【答案】D
【解析】∵A、B两点的纵坐标为0.
∴A、B为抛物线与x轴的交点，
∴△OBC为直角三角形。
又∵C点有可能在y轴的负半轴，也可能在y轴的正半轴。
∴C点的纵坐标为3或3(根据勾股定理求得).
∴C点的纵坐标为(0,3)或(0,3).
设函数的解析式为y=ax+bx+c，
(1)则当抛物线经过(1,0)、(3,0)、(0,3)三点时，
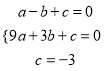解得：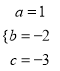 
，
则解析式为y=x2x3；
(2)则当抛物线经过(1,0)、(3,0)、(0,3)三点时，
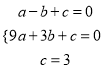解得：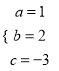 
，
则解析式为y=x+2x+3.
故选D.
练习册系列答案
阅读快车系列答案
相关题目
