题目内容
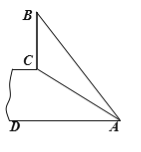
【题目】如图,斜坡AC的坡度(坡比)为1: ![]() ,AC=10米.坡顶有一垂直于水平面的旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度.
,AC=10米.坡顶有一垂直于水平面的旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度.
【答案】6米.
【解析】
试题分析:如果延长BC交AD于E点,则CE⊥AD,要求BC的高度,就要知道BE和CE的高度,就要先求出AE的长度.直角三角形ACE中有坡比,由AC的长,那么就可求出AE的长,然后求出BE、CE的高度,BC=BE-CE,即可得出结果.
试题解析:延长BC交AD于E点,则CE⊥AD.
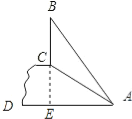
在Rt△AEC中,AC=10,由坡比为1:![]() 可知:∠CAE=30°,
可知:∠CAE=30°,
∴CE=ACsin30°=10×![]() =5,
=5,
AE=ACcos30°=10×![]() =5
=5![]() .
.
在Rt△ABE中,![]() .
.
∵BE=BC+CE,
∴BC=BE-CE=11-5=6(米).
答:旗杆的高度为6米.
考点: 解直角三角形的应用-坡度坡角问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


