题目内容
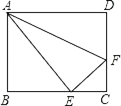
【题目】如图,在矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,求CF的长.
【答案】![]() .
.
【解析】
证△AEF≌△ADF,推出AE=AD=5,EF=DF,在△ABE中,由勾股定理求出BE=3,求出CE=2,设CF=x,则EF=DF=4﹣x,在Rt△CFE中,由勾股定理得出方程(4﹣x)2=x2+22,求出x即可.
∵AF平分∠DAE,
∴∠DAF=∠EAF,
∵四边形ABCD是矩形,
∴∠D=∠C=90°,AD=BC=5,AB=CD=4,
∵EF⊥AE,
∴∠AEF=∠D=90°,
在△AEF和△ADF中,
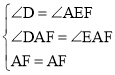 ,
,
∴△AEF≌△ADF(AAS),
∴AE=AD=5,EF=DF,
在△ABE中,∠B=90°,AE=5,AB=4,由勾股定理得:BE=3,
∴CE=5﹣3=2,
设CF=x,则EF=DF=4﹣x,
在Rt△CFE中,由勾股定理得:EF2=CE2+CF2,
∴(4﹣x)2=x2+22,
x=![]() ,
,
CF=![]() .
.

【题目】为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)求活动启动之初学生“一周诗词诵背数量”的中位数;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
【题目】随着气温的升高,空调的需求量大增.某家电超市对每台进价分别为2000元、1700元的![]() 、
、![]() 两种型号的空调,近两周的销售情况统计如下:
两种型号的空调,近两周的销售情况统计如下:
销售时段 | 销售量 | 销售收入 | |
|
| ||
第一周 | 6台 | 7台 | 31000元 |
第二周 | 8台 | 11台 | 45000元 |
(1)求![]() 、
、![]() 两种型号的空调的销售价;
两种型号的空调的销售价;
(2)若该家电超市准备用不多于54000元的资金,采购这两种型号的空调30台,求![]() 种型号的空调最多能采购多少台?
种型号的空调最多能采购多少台?
(3)在(2)的条件下,该家电超市售完这30台空调能否实现利润不低于15800元的目标?若能,请给出采购方案.若不能,请说明理由.