题目内容
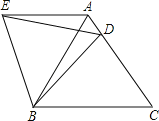
【题目】如图,已知∠COA=90°,∠COD比∠DOA大28°,且OB是∠COA的平分线.

(1)求∠BOD的度数;
(2)将已知条件中的28°改为32°,则∠BOD= ;
(3)将已知条件中的28°改为n°,则∠BOD= .
【答案】(1)14°; (2)16°;(3)(![]() )°.
)°.
【解析】
试题分析:(1)根据已知得出∠DOA+28°+∠DOA=90°,求出∠DOA,根据角平分线求出∠AOB,代入∠BOD=∠AOB﹣∠DOA求出即可;
(2)根据已知得出∠DOA+32°+∠DOA=90°,求出∠DOA,根据角平分线求出∠AOB,代入∠BOD=∠AOB﹣∠DOA求出即可;
(3)根据已知得出∠DOA+n°+∠DOA=90°,求出∠DOA,根据角平分线求出∠AOB,代入∠BOD=∠AOB﹣∠DOA求出即可.
解:(1)∵∠COD比∠DOA大28°,
∴∠COD=∠DOA+28°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+28°+∠DOA=90°,
∴∠DOA=31°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
=![]() ∠AOC
∠AOC
=45°,
∴∠BOD=∠AOB﹣∠DOA
=45°﹣31°
=14°;
(2)∵∠COD比∠DOA大32°,
∴∠COD=∠DOA+32°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+32°+∠DOA=90°,
∴∠DOA=29°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
=![]() ∠AOC
∠AOC
=45°,
∴∠BOD=∠AOB﹣∠DOA
=45°﹣29°
=16°;
故答案为:16°;
(3)∵∠COD比∠DOA大n°,
∴∠COD=∠DOA+n°,
∵∠AOC=90°,
∴∠COD+∠DOA=90°,
∴∠DOA+n°+∠DOA=90°,
∴∠DOA=(45﹣![]() )°,
)°,
∵OB是∠AOC的平分线,
∴∠AOB=∠BOC
=![]() ∠AOC
∠AOC
=45°,
∴∠BOD=∠AOB﹣∠DOA
=45°﹣(45﹣![]() )°
)°
=(![]() )°;
)°;
故答案为:(![]() )°.
)°.