题目内容
如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于C点,四边形OBHC为矩形,CH的延长
轴交于C点,四边形OBHC为矩形,CH的延长![]() 线交抛物线于点D(5,2),连结BC、AD.
线交抛物线于点D(5,2),连结BC、AD.
(1)求C点的坐标及抛物线的解析式;
(2)将△BCH绕点B按顺时针旋转90º后再沿![]() 轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
(3)设过点E的直线交AB边于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形ABCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.

解:(1)∵四边形OBHC为矩形,∴CD∥AB, 又D(5,2), ∴C(0,2),OC=2 . …1 分
 ∴
∴ 解得
解得
∴抛物线的解析式为:![]() …… 4分
…… 4分
(2)点E落在抛物线上. 理由如下:
由y = 0,得![]() .
.
解得x1=1,x2=4. ∴A(4,0),B(1,0). …… 5分 ∴OA=4,OB=1.
由矩形性质知:CH=OB=1,BH=OC=2,∠BHC=90°,
由旋转、轴对称性质知:EF=1,BF=2,∠EFB=90°, ∴点E的坐标为(3,-1).… 7分
把x=3代入![]() ,得
,得![]() , ∴点E在抛物线上. … 8分
, ∴点E在抛物线上. … 8分
(3)存在点P(a,0),延长EF交CD于点G,易求OF=CG=3,PB=a-1.
S梯形BCGF = 5,S梯形ADGF = 3,记S梯形BCQP = S1,S梯形ADQP = S2,
下面分两种情形: ①当S1∶S2 =1∶3时,![]() ,
,
此时点P在点F(3,0)的左侧,则PF = 3-a,
由△EPF∽△EQG,得![]() ,则QG=9-3a,∴CQ=3-(9-3a) =3a -6
,则QG=9-3a,∴CQ=3-(9-3a) =3a -6
由S1=2,得![]() ,解得
,解得![]() ; …… 10分
; …… 10分
②当S1∶S2=3∶1时,![]() , 此时点P在点F(3,0)的右侧,则PF = a-3,
, 此时点P在点F(3,0)的右侧,则PF = a-3,
由△EPF∽△EQG,得QG = 3a-9,∴CQ = 3 +(3 a-9)= 3 a-6,由S1= 6,
得![]() ,解得
,解得![]() .
.
综上所述:所求点P的坐标为(![]() ,0)或(
,0)或(![]() ,0)…… 12分
,0)…… 12分

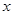 轴交于
轴交于 (2)点
(2)点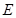 为抛物线上一动点,在
为抛物线上一动点,在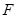 ,使以
,使以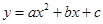 与
与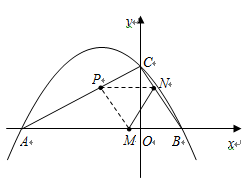
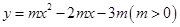 与
与 轴交于
轴交于 两点,与
两点,与 轴交于
轴交于 点.
点.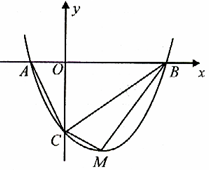
 的坐标(用含
的坐标(用含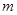 的代数式表示),
的代数式表示),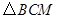 与
与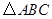 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;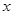 轴交于
轴交于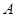 (
(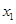 ,0)、
,0)、 (
(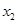 ,0)两点,且
,0)两点,且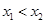 ,与
,与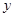 轴交于点
轴交于点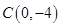 ,其中
,其中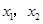 是方程
是方程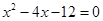 的两个根。(14分)
的两个根。(14分) (2)点
(2)点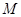 是线段
是线段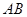 上的一个动点,过点
上的一个动点,过点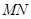 ∥
∥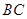 ,交
,交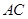 于点
于点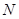 ,连接
,连接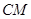 ,当
,当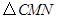 的面积最大时,求点
的面积最大时,求点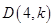 在(1)中抛物线上,
在(1)中抛物线上,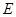 为抛物线上一动点,在
为抛物线上一动点,在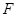 ,使以
,使以 为顶
为顶