题目内容
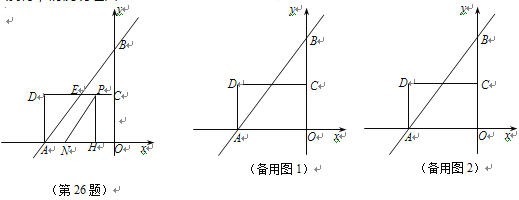
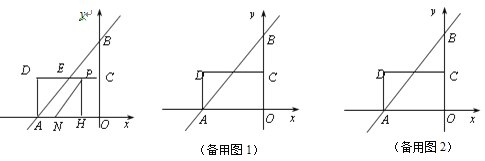
【题目】如图，在平面直角坐标系中，直线
分别交
轴，
轴于A，B两点，点C为OB的中点，点D在第二象限，且四边形AOCD为矩形．
（1）直接写出点A，B的坐标，并求直线AB与CD交点E的坐标；
（2）动点P从点C出发，沿线段CD以每秒1个单位长度的速度向终点D运动；同时，动点N从点A出发，沿线段AO以每秒1个单位长度的速度向终点O运动，过点P作
，垂足为H，连接NP．设点P的运动时间为t秒．
① 若△NPH的面积为1，求t的值；
② 点Q是点B关于点A的对称点，问
是否有最小值，如果有，求出相应的点P的坐标；如果没有，请说明理由．
【答案】(1)、A(－3,0)、B(0,4)；E(－
，2)；(2)、①、t=1或2；②、P(－2,2)
【解析】
试题分析：(1)、根据一次函数得出A、B两点的坐标，根据矩形的性质得出点E的坐标；(2)、设PC=t，AN=t，NO=3－t，首先求出t的取值范围，得到NH=3jain2t，然后利用面积求出t的值；根据题意得出点Q的坐标，作QQ′平行且等于PH，易证四边形QQ/PH为平行四边形，得到点Q′的坐标，然后设出直线BQ′的解析式，把点Q′的坐标代入求出k的值，然后得出点P的坐标.
试题解析：(1)、A(-3,0)，B(0,4) ∵C(0,2) ∴0C=2 ∵四边形ABCD是矩形 ∴AO∥CD
∴当y=2时，x=－
∴E(－,2)
(2)、①PC=t，AN=t，NO=3－t， 3－t＞t ∴t＜
当0＜t＜时，NH=3－t－t=3－2t ∴S=
×2×(3－2t)=1 解得：t=1
3－t＜t，∴t＞ 当＜t≤3 NH=2t－3 ∴S=×2×(2t－3)=1 解得：t=2
所以t=1或t=2
②易得Q(-6,-4)，作QQ′平行且等于PH，易证四边形QQ/PH为平行四边形， Q′（-6，-2）
设BQ′直线的解析式为y=kx+4(k≠0) 把Q′（-6，-2）代入得到k=1
当y=2时x=－2，此时t=2 故存在P（-2,2）
