Question

【题目】（探究）某商场秋季计划购进一批进价为每条40元的围巾进行销售，根据销售经验，应季销售时，若每条围巾的售价为60元，则可售出400条；若每条围巾的售价每提高1元，销售量相应减少10条．

（1）假设每条围巾的售价提高x元，那么销售每条围巾所获得的利润是________元，销售量是______条；（用含x的代数式表示）

（2）设应季销售利润为y元，请写y与x的函数关系式；并求出应季销售利润为8000元时每条围巾的售价；

（拓展）根据销售经验，过季处理时，若每条围巾的售价定为30元亏本销售，可售出50条；若每条围巾的售价每降低1元，销售量相应增加5条．

（1）若剩余100条围巾需要处理，经过降价处理后还是无法销售的只能积压在仓库，损失本金；若使亏损金额最小，求每条围巾的售价；

（2）若过季需要处理的围巾共m条，且，求过季亏损金额最小值；（用含m的代数式表示）

（延伸）若商场共购进了500条围巾且销售情况满足上述条件，如果应季销售利润在不低于8000元的条件下：

（1）没有售出的围巾共m条，求m的取值范围；

（2）要使最后的总利润（销售利润=应季销售利润-过季亏损金额）最大，求应季销售的售价．

参考公式：抛物线的顶点坐标是．

Answer 1

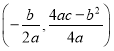【答案】【探究】（1）；；（2）围巾的售价为60元或80元；【拓展】（1）亏损金额最小为2000元，此时售价为元/件；（2）时亏损金额最少，最小值为；【延伸】（1）；（2）应季售价为60元/条，总利润w有最大值6000元

【解析】

【探究】（1）；；

（2）由题意得：，

把代入得，

解得，

答：围巾的售价为60元或80元；

【拓展】（1）设过季处理时亏损金额为元，单价降低z元．

由题意得：

，

∵，对称轴，

∴当时，

（元），

∴亏损金额最小为2000元，此时售价为（元/件）；

（2），

，

∵，∴时亏损金额最少，最小值为；

【延伸】（1）m的取值范围是：；

（2）∵，且，

∴亏损的最小金额为：

（元）．

设总利润为w，则

．

∵，对称轴，

∴当时，w随x的增大而减小，

∴当时，即应季售价为60元/条，总利润w有最大值6000元．