题目内容
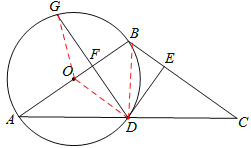
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,DE⊥BC,垂足为E.

(1)求证:DE是⊙O的切线;
(2)若DG⊥AB,垂足为点F,交⊙O于点G,∠A=35°,⊙O半径为5,求劣弧DG的长.(结果保留π)
【答案】解:(1)证明:连接BD、OD,
∵AB是⊙O直径,∴∠ADB=90°。∴BD⊥AC。
∵AB=BC,∴AD=DC。
∵AO=OB,∴DO∥BC。
∵DE⊥BC,∴DE⊥OD。
∵OD为半径,∴DE是⊙O切线。
(2)连接OG,
∵DG⊥AB,OB过圆心O,∴弧BG=弧BD。
∵∠A=35°,∴∠BOD=2∠A=70°。∴∠BOG=∠BOD=70°。∴∠GOD=140°。
∴劣弧DG的长是![]() 。
。
【解析】
试题(1)连接BD,OD,求出OD∥BC,推出OD⊥DE,根据切线判定推出即可。
(2)求出∠BOD=∠GOB,从而求出∠BOD的度数,根据弧长公式求出即可。

练习册系列答案
相关题目