题目内容
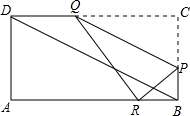
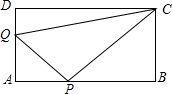
如图所示，在矩形ABCD中，AB=12厘米，BC=6厘米，点P沿AB边从点A开始向点B以2厘米/秒的速度移动；点Q沿DA边从点D向点A以1厘米/秒的速度移动．如果P、Q同时
出发，用t（秒）表示移动时间（0≤t≤6）．那么：
（1）当t为何值时，△QAP为等腰直角三角形？
（2）当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似？
出发，用t（秒）表示移动时间（0≤t≤6）．那么：（1）当t为何值时，△QAP为等腰直角三角形？
（2）当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似？
分析：（1）根据题意得出DQ=t，AP=2t，QA=6-t，由于△QAP为等腰直角三角形，则6-t=2t，求出t的值即可；
（2）由于以点Q、A、P为顶点的三角形与△ABC的对应边不能确定，故应分两种情况进行讨论．
（2）由于以点Q、A、P为顶点的三角形与△ABC的对应边不能确定，故应分两种情况进行讨论．
解答：解：（1）∵AB=12厘米，BC=6厘米，点P沿AB边从点A开始向点B以2厘米/秒的速度移动；点Q沿DA边从点D向点A以1厘米/秒的速度移动，
∴DQ=t，AP=2t，QA=6-t，
当△QAP为等腰直角三角形即6-t=2t，解得t=2；
（2）两种情况：
当
=
时，即
=
，解得t=1.2（秒）；
当
=
时，即
=
，解得t=3（秒）．
故当经过1.2秒或3秒时，△QAP与△ABC相似．
∴DQ=t，AP=2t，QA=6-t，
当△QAP为等腰直角三角形即6-t=2t，解得t=2；
（2）两种情况：
当
| AQ |
| AB |
| AP |
| BC |
| 6-t |
| 12 |
| 2t |
| 6 |
当
| AQ |
| BC |
| AP |
| AB |
| 6-t |
| 6 |
| 2t |
| 12 |
故当经过1.2秒或3秒时，△QAP与△ABC相似．
点评：本题考查的是相似三角形的性质及等腰直角三角形的性质，熟知相似三角形的对应边成比例是解答此题的关键．
练习册系列答案
相关题目
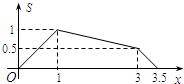
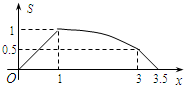
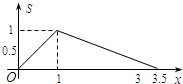
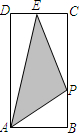如图所示，在矩形ABCD中，AB=1，BC=2，E是CD边的中点．点P从点A开始，沿逆时针方向在矩形边上匀速运动，到点E停止．设点P经过的路程为x，△APE的面积为S，则S关于x的函数关系的大致图象是（ ）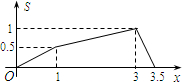
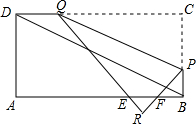
P也随之停止运动．用t表示移动时间，设四边形QAPC的面积为S．
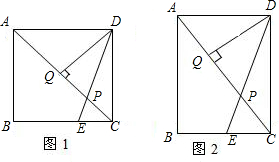B=nBC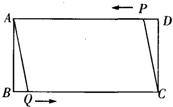
如图所示，在矩形ABCD中，AB=4cm，BC=8cm、点P从点D出发向点A运动，同时点Q从点B出发向点C运动，点P、Q的速度都是1cm/s．