题目内容
如图所示,在矩形ABCD中,E为BC上一动点,BE=kCE,ED交AC于点P,DQ⊥AC于Q,A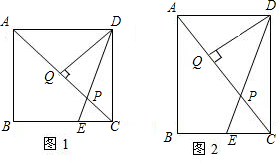 B=nBC
B=nBC(1)当n=1,k=2时(如图1),
| CP |
| PQ |
(2)当n=
| 2 |
(3)若k=1,当n=
分析:(1)根据题意可以得出Q为正方形的中点,AQ=CQ,结合△ADP∽△CEP,得出CP和AP的关系,即可得出结论.
(2)同(1)得出CP和AP的关系,设BC=1,则AB=
,进而得出AC的长,由条件可以证得△ADQ∽△CAB,即得出AD、CA、AQ、BC之间的关系式,求出AQ的值,即可证得.
(3)把结论当做已知条件,可得△CPE∽△CBA,求得CE、CP、CA、CB之间的关系式,设BC=1,则可以表示出AB、AC、PC的值,代入关系式求解即可.
(2)同(1)得出CP和AP的关系,设BC=1,则AB=
| 2 |
(3)把结论当做已知条件,可得△CPE∽△CBA,求得CE、CP、CA、CB之间的关系式,设BC=1,则可以表示出AB、AC、PC的值,代入关系式求解即可.
解答:解:(1)∵矩形ABCD中,AB=AC,
∴AD=BC、AD∥BC,OA=OC,
∴∠DAP=∠ECP,∠ADP=∠CPE,
∴△ADP∽△CEP,
∴
=
,
∵BE=kCE,k=2,
∴AD:CE=3:1,
∴AP:CP=3:1,
∴
=1.
(2)证明:∵矩形ABCD中,BE=kCE,AB=nBC,n=
,k=1,
∴AD∥BC,AD=BC,∠DAP=∠ECP,∠ADP=∠CEP,
∴△ADP∽△CEP,
∴
=
=
,
设BC=1,则AB=
,根据勾股定理得AC=
,PC=
∵DAQ=∠BCA、∠AQD=∠B=90°,
∴△ADQ∽△CAB,
∴
=
=
,
∴AQ=
,
∴CP=AQ.
(3)∵矩形ABCD中,BE=kCE,AB=nBC,k=1,
∴AD∥BC,AD=BC,∠DAP=∠ECP,∠ADP=∠CEP,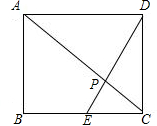
∴
=
=
,
设BC=1,则AB=n,AC=
,
∴PC=
,
∵CP⊥DE,
∴∠CPE=∠CBA,
∵∠ECP=∠ACB,
∴△CPE∽△CBA,
∴
=
,
∴
=
,
∴n=
.
∴AD=BC、AD∥BC,OA=OC,
∴∠DAP=∠ECP,∠ADP=∠CPE,
∴△ADP∽△CEP,
∴
| AP |
| CP |
| AD |
| CE |
∵BE=kCE,k=2,
∴AD:CE=3:1,
∴AP:CP=3:1,
∴
| CP |
| PQ |
(2)证明:∵矩形ABCD中,BE=kCE,AB=nBC,n=
| 2 |
∴AD∥BC,AD=BC,∠DAP=∠ECP,∠ADP=∠CEP,
∴△ADP∽△CEP,
∴
| AD |
| CE |
| AP |
| CP |
| 2 |
| 1 |
设BC=1,则AB=
| 2 |
| 3 |
| ||
| 3 |
∵DAQ=∠BCA、∠AQD=∠B=90°,
∴△ADQ∽△CAB,
∴
| AQ |
| BC |
| AD |
| AC |
| 1 | ||
|
∴AQ=
| ||
| 3 |
∴CP=AQ.
(3)∵矩形ABCD中,BE=kCE,AB=nBC,k=1,
∴AD∥BC,AD=BC,∠DAP=∠ECP,∠ADP=∠CEP,

∴
| AD |
| CE |
| AP |
| CP |
| 2 |
| 1 |
设BC=1,则AB=n,AC=
| 1+n2 |
∴PC=
| ||
| 3 |
∵CP⊥DE,
∴∠CPE=∠CBA,
∵∠ECP=∠ACB,
∴△CPE∽△CBA,
∴
| CE |
| AC |
| CP |
| BC |
∴
| ||
|
| ||||
| 1 |
∴n=
| ||
| 2 |
点评:本题考查了矩形的性质,综合运用了三角形相似的性质,属于基本的题型,要求熟练掌握.

练习册系列答案
相关题目
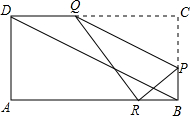
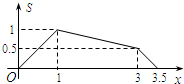
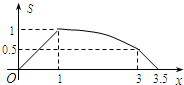
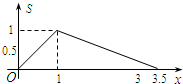
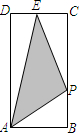 如图所示,在矩形ABCD中,AB=1,BC=2,E是CD边的中点.点P从点A开始,沿逆时针方向在矩形边上匀速运动,到点E停止.设点P经过的路程为x,△APE的面积为S,则S关于x的函数关系的大致图象是( )
如图所示,在矩形ABCD中,AB=1,BC=2,E是CD边的中点.点P从点A开始,沿逆时针方向在矩形边上匀速运动,到点E停止.设点P经过的路程为x,△APE的面积为S,则S关于x的函数关系的大致图象是( )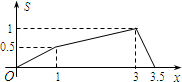
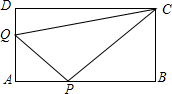 P也随之停止运动.用t表示移动时间,设四边形QAPC的面积为S.
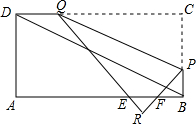
P也随之停止运动.用t表示移动时间,设四边形QAPC的面积为S. 如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.
如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.