题目内容
如图,在3×3的方格中(每个小正方形的边长为1)四边形ABCD是正方形,利用面积的关系探求正方形ABCD的边长是 .


首先用大正方形的面积减去4个小直角三角形的面积,求得正方形ABCD的面积,又由正方形的面积是边长的平方,求正方形ABCD的面积的算术平方根即可.
解:∵S正方形ABCD=S正方形EFGH-S△ADE-S△AFB-S△BGC-S△CHD

=3×3- ×2×1-
×2×1- ×2×1-
×2×1- ×2×1-
×2×1- ×2×1
×2×1
=9-1-1-1-1=5,
∴AD= .
.
即正方形ABCD的边长是
故答案为 .
.
解:∵S正方形ABCD=S正方形EFGH-S△ADE-S△AFB-S△BGC-S△CHD

=3×3-
 ×2×1-
×2×1- ×2×1-
×2×1- ×2×1-
×2×1- ×2×1
×2×1=9-1-1-1-1=5,
∴AD=
 .
.即正方形ABCD的边长是

故答案为
 .
.
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目

 ,
, ABCD的
ABCD的 各边AB、BC、CD、DA上,分别取点K、L、M、N,使A
各边AB、BC、CD、DA上,分别取点K、L、M、N,使A K=CM、BL=DN,求证:四边形KLMN为平行四边形。
K=CM、BL=DN,求证:四边形KLMN为平行四边形。
 中,
中, 为
为 上一点,且
上一点,且 .
. 为等腰直角三角形,斜边
为等腰直角三角形,斜边 与
与 交于点
交于点 ,延长
,延长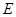 ,连接
,连接 、
、 ,作
,作 ,垂足为
,垂足为 ,下列结论:①
,下列结论:① ≌
≌ ;②
;② 为等腰直角三角形;③
为等腰直角三角形;③ ;④
;④ ;⑤
;⑤ .其中正确的个数为( )
.其中正确的个数为( )


 中,
中, ∥
∥ ,点
,点 在
在 上,点
上,点 在
在 上,
上, 是中位线,若
是中位线,若 ,
, ,则用
,则用 、
、 表示
表示 _______
_______
 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.