题目内容
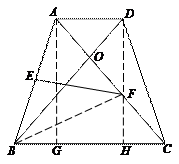
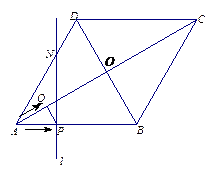
如图,等腰梯形ABCD中,AB = CD,AD∥BC.

(1)求证:△AOB≌△DOC;
(2)若AD = 4,BC = 8, ,
,
①求梯形ABCD的面积;
②若E为AB中点,F为OC的中点,求EF的长.

(1)求证:△AOB≌△DOC;
(2)若AD = 4,BC = 8,
 ,
,①求梯形ABCD的面积;
②若E为AB中点,F为OC的中点,求EF的长.
(1) 证明:∵ 等腰梯形ABCD
∴ AB = CD,AC = BD
 ∵ BC = CB
∵ BC = CB
∴ △ABC≌△DCB(SSS)
∴ ∠BAC =∠CDB
∵ AB = CD
又 ∵ ∠AOB =∠DOC
∴ △AOB≌△DOC(AAS)
(2) 解:①过点A作AG⊥BC
∵ △AOB≌△DOC
∴ AO = DO,BO = CO
又 ∵ ∠AOB =∠BOC = 60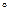
∴ △AOB、△DOC为等边三角形
∴ DO =" AD" = 4,CO = B C = 8
C = 8
∴ AC =" AO" + CO = 12
∵ ∠OCB = 60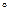 ,∴∠CAG = 30
,∴∠CAG = 30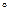
∴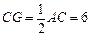
在 Rt△AGC中,
Rt△AGC中,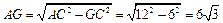
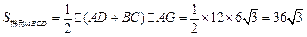
②连结BF,过D作DH⊥BC,交BC于点H
∴ GH =" AD" = 4,BG =" CH" =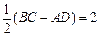
在Rt△ABG中,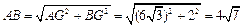
∵ △ BOC为等边三角形,F是OC的中点
∴ BF⊥AC
在Rt△AFB中,∵ E是AB的中点
∴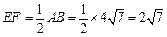
∴ AB = CD,AC = BD
 ∵ BC = CB
∵ BC = CB∴ △ABC≌△DCB(SSS)
∴ ∠BAC =∠CDB
∵ AB = CD
又 ∵ ∠AOB =∠DOC
∴ △AOB≌△DOC(AAS)
(2) 解:①过点A作AG⊥BC

∵ △AOB≌△DOC
∴ AO = DO,BO = CO
又 ∵ ∠AOB =∠BOC = 60
∴ △AOB、△DOC为等边三角形
∴ DO =" AD" = 4,CO = B
 C = 8
C = 8∴ AC =" AO" + CO = 12
∵ ∠OCB = 60
 ,∴∠CAG = 30
,∴∠CAG = 30
∴
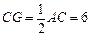
在
 Rt△AGC中,
Rt△AGC中,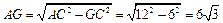
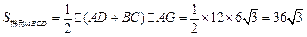
②连结BF,过D作DH⊥BC,交BC于点H
∴ GH =" AD" = 4,BG =" CH" =
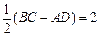
在Rt△ABG中,
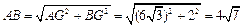
∵ △ BOC为等边三角形,F是OC的中点
∴ BF⊥AC
在Rt△AFB中,∵ E是AB的中点
∴
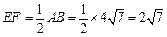
略

练习册系列答案
相关题目

 的边长为
的边长为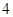 cm,正方形
cm,正方形 的边长为
的边长为 cm.如果正方形
cm.如果正方形 旋转,那么
旋转,那么 、
、 两点之间的最小距离是____________.
两点之间的最小距离是____________.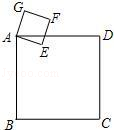
 否存在这样的t,使得△PMN是以PN为一直角边的
否存在这样的t,使得△PMN是以PN为一直角边的 直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由. ,AB =" 4" cm.那么,菱形ABCD的对角线AC的长为_____cm
,AB =" 4" cm.那么,菱形ABCD的对角线AC的长为_____cm
 )
)

 上的点,且△ACE是等边三角形.
上的点,且△ACE是等边三角形.