题目内容
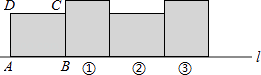
【题目】用火柴拼成如图所示的几何图形。图1有6根火柴棒拼成,图2有11根火柴棒拼成,图3由16根拼成······

图1 图2 图3
(1)图4由__________根火柴棒拼成;
(2)根据规律猜想,图n由________根火柴棒拼成;(用含n的代数式表示,不用说明理由)
(3)是否存在图x恰好由2017根火柴棒拼成?若存在,求出x的值;若不存在,请说明理由.
【答案】(1)21;(2)5n+1;(3)不存在,理由见解析.
【解析】试题分析: (1)根据图形发现:每多一个正方形就多用5根火柴棒,由此计算得出答案即可;
(2)利用(1)中的计算规律得出答案即可;
(3)把数据代入(2)中的式子计算得出答案即可.
试题解析:
(1)第4个图有5×4+1=21根火柴棒;
(2)当n=1时,火柴的根数是5×1+1=6;
当n=2时,火柴的根数是5×2+1=11;
当n=3时,火柴的根数是5×3+1=16;
…
所以第n个图形中火柴的根数有5n+1.
(3)不存在.理由:根据题意5x+1=2017.
解得![]() ,
,
因为![]() 不是正整数,
不是正整数,
所以不存在图![]() 恰好由2017根火柴棒拼成.
恰好由2017根火柴棒拼成.
点睛: 本题主要考查了图形的规律性问题,能够找出其中隐藏的内在规律并熟练求解.根据题干已知三角形需要的小棒个数,推理得出一般的规律特点,是解决此类问题的关键.

练习册系列答案
相关题目