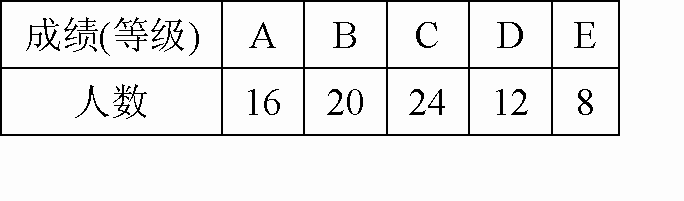题目内容
 为了了解某市参加2013年中考50000名初中毕业生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段统计如下:
为了了解某市参加2013年中考50000名初中毕业生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段统计如下:
| 分数段 | 人数(人) | 频率 |
| A:50分 | 48 | 0.2 |
| B:49-45分 | 60 | a |
| C:44-40分 | 84 | 0.35 |
| D:39-30分 | b | 0.15 |
| E:29-0分 | 12 | 0.05 |
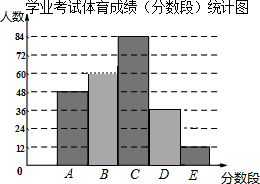
(1)在频数分布表中,a的值为______,b的值为______,并将频数分布直方图补充完整;
(2)在这个问题中,总体和样本容量分别是什么?
(3)若把40分以上(含40分)定为优秀,那么该市初中毕业生中体育成绩优秀的学生有多少人?
 解:(1)0.2+a+0.35+0.15+0.05=1,
解:(1)0.2+a+0.35+0.15+0.05=1,解得a=0.25,
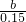 =
= ,
,解得b=36.
补全统计图如图所示:
(2)总体:50000名初中毕业生学业考试体育成绩;
样本容量:12÷0.05=240;
(3)50000×(0.2+0.25+0.35)=50000×0.8=40000(名).
故答案为:0.25,36.
分析:(1)根据频率之和等于1列式求解即可得到a的值,再根据频数与频率之比相等列式计算即可求出b值;
(2)根据总体的定义解答;
用E组的频数除以频率计算即可求出样本容量;
(3)用总人数乘以A、B、C组的频率之和,计算即可得解.
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
相关题目
某市七年级有15 000名学生参加安全知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分(得分取正整数,满分100分)进行统计,得到以下统计图表.
频数分布表 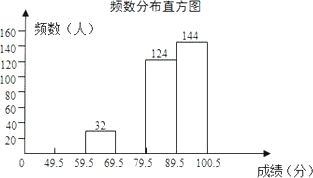
| 分组 | 频数 | 百分比 |
| 49.5~59.5 | 20 | 5% |
| 59.5~69.5 | 32 | 8% |
| 69.5~79.5 | 20% | |
| 79.5~89.5 | 124 | |
| 89.5~100.5 | 144 | 36% |
| 合计 | 400 | 100% |
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)此次竞赛七年级约有多少人在90分以上?
某市七年级有15000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分(得分取正整数,满分100分)进行统计:
频 率 分 布 表
| 分 组 | 频 数 | 频 率 |
| 49.5~59.5 | 20 | |
| 59.5~69.5 | 32 | 0.08 |
| 69.5~79.5 | 0.20 | |
| 79.5~89.5 | 124 | 0.31 |
| 89.5~100.5 | 144 | 0.36 |
| 合 计 | 400 | 1 |
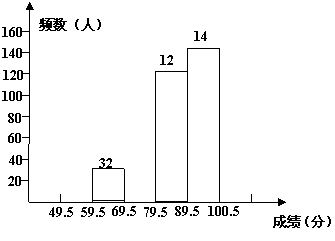
请你根据不完整的频率分布表,解答下列问题:
(1)补全频率分布表和频数分布直方图;
(2)若将得分转化为等级,规定得分低于59.5分评为“D”,59.5~69.5分评为“C”,
69.5~89.5分评为“B”,89.5~100.5分评为“A”,这次15000名学生中约有多少人评为“D”?
(3)以(2)的等级为标准,如果随机抽取一名参赛学生的成绩等级,则这名学生的成绩评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由.
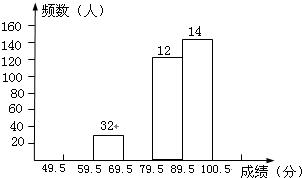
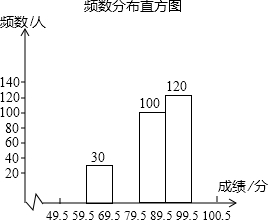 分100)进行统计:
分100)进行统计: