Question

【题目】阅读理解题

定义：如果四边形的某条对角线平分一组角，那么把这条对角线叫“美妙线”，该四边形叫做“美妙四边形”.

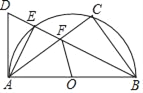
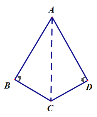
如图：在四边形ABCD中，对角线BC平分∠ACD和∠ABD,那么对角线BC叫“美妙线”，四边形ABCD就称为“美妙四边形”.

问题：（1）下列四边形中是“美妙四边形”的有_______个.

①平行四边形 ②矩形 ③菱形 ④正方形

A.1 B. 2 C. 3 D.4

（2）四边形ABCD是“美妙四边形”,AB=3+,∠BAD=60°,∠ABC=90°，求四边形ABCD的面积.

（3）如图，若△ABC中，AB=3，BC=4，∠B=90°，将△ABC扩充成以AC为“美妙线”的“美妙四边形”ABCD,试求D到BC的距离.

Answer 1

【答案】（1）B；（2）①S=②S=；（3）

【解析】

（1）根据“美妙四边形”的定义，结合平行四边形，矩形，菱形 ，正方形的性质即可判断.

(2)分①当AC是美妙线时和②当BD是美妙线时，两种情况进行讨论.

（3）如图，过D作MN∥BC交BA延长线于点M且CN⊥MN，证明△MDA∽△NCD

根据相似三角形的性质得到设AM=3x,则DN=4x,MD=4-4x,CN=3x+3，得到，解方程求出的值，即可求解.

.解：(1)菱形和正方形是“美妙四边形”.

故答案为：B

(2)①当AC是美妙线时，如图

AB=3+,∠BAD=60°,

，

，

②当BD是美妙线时，如图,过D作DH⊥AB,

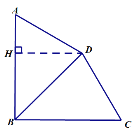
设AH=a,则

∴

∴

∴DH=3,

，

综上所述：S=或

（3）如图，过D作MN∥BC交BA延长线于点M且CN⊥MN

由题意，得∠M=∠N=90°

∠MDA+∠MAD=90°

∠MDA+∠CDN=90°

∴∠MAD=∠CDN

∴△MDA∽△NCD

设AM=3x,则DN=4x,MD=4-4x,CN=3x+3

∴x=，

∴DH=3x+3=