题目内容
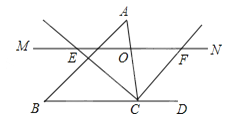
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?
并说明理由.
【答案】(1)证明见解析;(2)5;(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.证明见解析.
【解析】试题分析:(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案;(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可得出CO的长;(3)根据平行四边形的判定以及矩形的判定得出即可.
试题解析:(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF=![]() =10,
=10,
∴OC=![]() EF=5;
EF=5;
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超出或不足的部分分别用正数、负数来表示,记录如下表:若每袋标准质量为450g,则这批样品的总质量是多少?
与标准质量的差值(单位:g) | -3 | -2 | 0 | 1 | 1.5 | 2.5 |
袋数(单位:袋) | 1 | 4 | 3 | 4 | 5 | 3 |
【题目】下表记录了甲、乙、丙、丁四名八年级学生最近几次校数学竞赛成绩的平均数与方差:
甲 | 乙 | 丙 | 丁 | |
平均数(分) | 115 | 110 | 115 | 110 |
方差 | 3.4 | 3.4 | 7.3 | 8.5 |
根据表中数据,要从中选择一名成绩好且发挥稳定的学生参加市数学竞赛,应该选择( )
A.甲B.乙C.丙D.丁
