题目内容
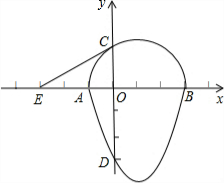我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图，点A，B，C，D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0，-3），AB为半圆的直径，半圆圆心M的坐标为（1，0），半圆半径为2，则经过点C的“蛋圆”切线EC的解析式是分析：根据题意，先求得C点坐标，然后根据三角形性质求出E点坐标，用待定系数法求出直线EC的解析式．
解答：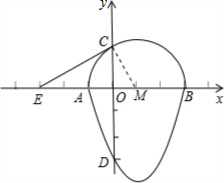
解：连接CM
在Rt△MOC中，∵OM=1，CM=2，
∴∠CMO=60°，OC=
，即C的坐标为（0，
）；
在Rt△MCE中，∵MC=2，∠CMO=60°，
∴ME=4，即E的坐标分别为（-3，0）．
故设EC的解析式为y=kx+
，把E点坐标代入得：k=
，
故EC的解析式是y=
x+
．
解：连接CM在Rt△MOC中，∵OM=1，CM=2，
∴∠CMO=60°，OC=
| 3 |
| 3 |
在Rt△MCE中，∵MC=2，∠CMO=60°，
∴ME=4，即E的坐标分别为（-3，0）．
故设EC的解析式为y=kx+
| 3 |
| ||
| 3 |
故EC的解析式是y=
| ||
| 3 |
| 3 |
点评：本题考查学生数形结合处理问题、解决问题的能力．
练习册系列答案
相关题目
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图，点A、B、C、D分别是“蛋圆”与坐标轴的交点，点D的坐标为（0，-3）AB为半圆直径，半圆圆心M（1，0），半径为2，则“蛋圆”的抛物线部分的解析式为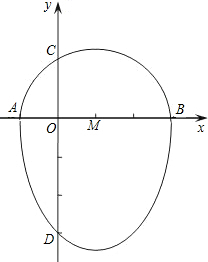
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”，如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图所示，点A、B、C、D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0，-3），AB为半圆的直径，半圆圆心M的坐标为（1，0），半圆半径为2．
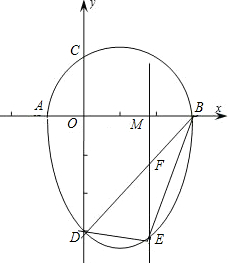正确？提出你的见解，若△BDE的面积存在最大值，请求出m的值以及点E的坐标．
仔细阅读并完成下题：