题目内容
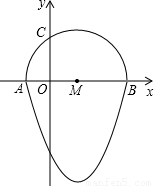
仔细阅读并完成下题：我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”；如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．如图，已知“蛋圆”是由抛物线y=ax2-2ax+c的一部分和圆心为M的半圆合成的．点A、B、C分别是“蛋圆”与坐标轴的交点，已知点A的坐标为（-1，0），AB为半圆的直径，
（1）点B的坐标为（
3
3
，0
0
）；点C的坐标为（0
0
，| 3 |
| 3 |
2
2
；（2）若P是“蛋圆”上的一点，且以O、P、B为顶点的三角形是等腰直角三角形求符合条件的点P的坐标，以及所对应的a的值；
（3）已知直线y=x-
| 7 |
| 2 |
分析：（1）由新定义的“蛋圆”图形不难看出：“蛋圆”是一个轴对称图形，对称轴与抛物线相同，因此圆心M在抛物线的对称轴上，首先由抛物线的解析式确定点M的坐标，再由A、B关于点M对称求出点B的坐标，则半圆的半径可求；连接CM，在Rt△OCM中，CM是半圆的半径，OM是点M横坐标的绝对值，由勾股定理即可求得OC的长，则点C的坐标可求．
（2）首先将点A或点B的坐标代入抛物线的解析式中，求出a、c的数量关系，目标是令抛物线的解析式中只有一个待定系数a；通过观察图形不难看出：点B不可能是直角顶点，因此只考虑两种情况：点O是直角顶点、点P是直角顶点；
Ⅰ、当点P在半圆上时，若存在符合条件的点P，那么a只要大于0就符合题干的要求，需要分两种情况讨论：
①若点O为直角顶点，那么点P为半圆与y轴的交点，显然由（1）的结论可以判断出OB、OC是否为相等关系，若相等，那么点C就符合点P的要求，若不相等，那么这种情况不予考虑；
②若点P为直角顶点，那么作OB的中垂线，若存在符合条件的点P，那么点P必为中垂线与半圆的交点，可以通过勾股定理求出该点到x轴的距离，然后判断此距离是否为OB的一半即可．
Ⅱ、当点P在抛物线上时，若能求得符合条件的点P，可以代入抛物线的解析式中求出a的值；分两种情况讨论：
①若点O为直角顶点，同Ⅰ-①先求出点P的坐标，再代入抛物线的解析式中确定a的值；
②若点P为直角顶点，首先根据等腰直角三角形的性质确定点P的坐标（等腰直角三角形斜边上的高等于斜边的一半），然后代入抛物线的解析式中求解即可．
（3）联立直线和抛物线的解析式，消去y后，令所得的一元二次方程的根的判别式为0，即可求出a的值．
（2）首先将点A或点B的坐标代入抛物线的解析式中，求出a、c的数量关系，目标是令抛物线的解析式中只有一个待定系数a；通过观察图形不难看出：点B不可能是直角顶点，因此只考虑两种情况：点O是直角顶点、点P是直角顶点；
Ⅰ、当点P在半圆上时，若存在符合条件的点P，那么a只要大于0就符合题干的要求，需要分两种情况讨论：
①若点O为直角顶点，那么点P为半圆与y轴的交点，显然由（1）的结论可以判断出OB、OC是否为相等关系，若相等，那么点C就符合点P的要求，若不相等，那么这种情况不予考虑；
②若点P为直角顶点，那么作OB的中垂线，若存在符合条件的点P，那么点P必为中垂线与半圆的交点，可以通过勾股定理求出该点到x轴的距离，然后判断此距离是否为OB的一半即可．
Ⅱ、当点P在抛物线上时，若能求得符合条件的点P，可以代入抛物线的解析式中求出a的值；分两种情况讨论：
①若点O为直角顶点，同Ⅰ-①先求出点P的坐标，再代入抛物线的解析式中确定a的值；
②若点P为直角顶点，首先根据等腰直角三角形的性质确定点P的坐标（等腰直角三角形斜边上的高等于斜边的一半），然后代入抛物线的解析式中求解即可．
（3）联立直线和抛物线的解析式，消去y后，令所得的一元二次方程的根的判别式为0，即可求出a的值．
解答：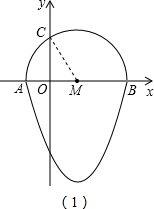
解：（1）由抛物线y=ax2-2ax+c知，对称轴 x=1；
∴点M的坐标为（1，0）；
∵点A、B关于点M对称，且A（-1，0）、M（1，0）
∴B（3，0），半圆的半径 r=AM=BM=2；
连接CM，在Rt△OCM中，CM=r=2，OM=1，OC=
=
=
，即 C（0，
）；
故答案：B（3，0）、C（0，
），半圆M的半径为2．
（2）因为抛物线y=ax2-2ax+c经过A（-1，0），有：
a+2a+c=0，c=-3a
∴抛物线：y=ax2-2ax-3a；
Ⅰ、当点P在半圆上时；
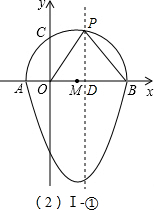
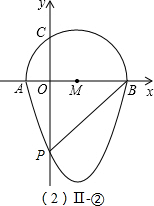
①点P是直角顶点，如右图（图Ⅰ-①）；
若△OBP是等腰直角三角形，那么点P必在OB的中垂线上，即 AD=BD=PD=
；
在Rt△OPD中，OP=2，OD=
，则 PD=
=
≠
，
线段PD长的前后结论矛盾，所以这种情况不成立；
②点O是直角顶点；
由（1）知：OC=
＜OB，因此这种情况也不成立．
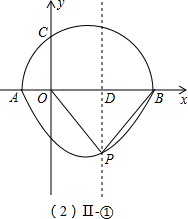Ⅱ、点P在抛物线上时；
①点P是直角顶点，如右图（图Ⅱ-①）；
若△OPB是等腰直角三角形，则 OD=BD=PD=
，即 P（
，-
）；
将点P的坐标代入y=ax2-2ax-3a中，有：
a×（
）2-2a×
-3a=-
，
解得：a=
；
②点O是直角顶点，那么点P必为抛物线与y轴的交点（如图Ⅱ-②）；
若△OPB为等腰直角三角形，则 OP=OB=3，即 P（0，-3）；
同①，求得：a=1．
综上，当P（0，-3）时，a=1；当P（
，-
）时，a=
．
（3）联立直线y=x-
与抛物线y=ax2-2ax-3a，有：
x-
=ax2-2ax-3a，
化简，得：ax2-（2a+1）x-3a+
=0
∴△=（2a+1）2-4a（-3a+
）=16a2-10a+1=0，
解得：a=
或a=
；
∴满足条件的抛物线的解析式为：y=
x2-x-
、y=
x2-
x-
．
解：（1）由抛物线y=ax2-2ax+c知，对称轴 x=1；∴点M的坐标为（1，0）；
∵点A、B关于点M对称，且A（-1，0）、M（1，0）
∴B（3，0），半圆的半径 r=AM=BM=2；
连接CM，在Rt△OCM中，CM=r=2，OM=1，OC=
| CM2-OM2 |
| 22-12 |
| 3 |
| 3 |
故答案：B（3，0）、C（0，
| 3 |
（2）因为抛物线y=ax2-2ax+c经过A（-1，0），有：
a+2a+c=0，c=-3a
∴抛物线：y=ax2-2ax-3a；Ⅰ、当点P在半圆上时；
①点P是直角顶点，如右图（图Ⅰ-①）；
若△OBP是等腰直角三角形，那么点P必在OB的中垂线上，即 AD=BD=PD=
| 3 |
| 2 |
在Rt△OPD中，OP=2，OD=
| 3 |
| 2 |
| OP2-OD2 |
22-(
|
| 3 |
| 2 |
线段PD长的前后结论矛盾，所以这种情况不成立；
②点O是直角顶点；
由（1）知：OC=
| 3 |
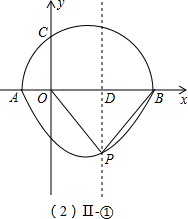Ⅱ、点P在抛物线上时；①点P是直角顶点，如右图（图Ⅱ-①）；
若△OPB是等腰直角三角形，则 OD=BD=PD=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
将点P的坐标代入y=ax2-2ax-3a中，有：
a×（
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解得：a=
| 2 |
| 5 |
②点O是直角顶点，那么点P必为抛物线与y轴的交点（如图Ⅱ-②）；
若△OPB为等腰直角三角形，则 OP=OB=3，即 P（0，-3）；
同①，求得：a=1．
综上，当P（0，-3）时，a=1；当P（| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
| 5 |
（3）联立直线y=x-
| 7 |
| 2 |
x-
| 7 |
| 2 |
化简，得：ax2-（2a+1）x-3a+
| 7 |
| 2 |
∴△=（2a+1）2-4a（-3a+
| 7 |
| 2 |
解得：a=
| 1 |
| 2 |
| 1 |
| 8 |
∴满足条件的抛物线的解析式为：y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 8 |
| 1 |
| 4 |
| 3 |
| 8 |
点评：该题给出了一个新图形的定义，但归根到底还是圆和二次函数的综合题；主要涉及的考点有：圆和抛物线的对称性、直线与抛物线交点个数的确定方法、等腰直角三角形的判定和性质等；题目的难点是第二小题，涉及的情况较多，需要分类讨论；需要注意的是，由于题干给出的是“点P在‘蛋圆’上”，因此点P在半圆上的情况也需要进行讨论．
练习册系列答案
相关题目
仔细阅读并完成下题：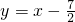
是“蛋圆”的切线，求满足条件的抛物线解析式．