题目内容
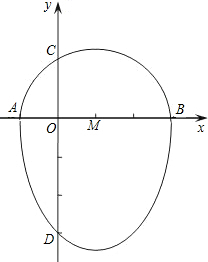
 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3)AB为半圆直径,半圆圆心M(1,0),半径为2,则“蛋圆”的抛物线部分的解析式为
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3)AB为半圆直径,半圆圆心M(1,0),半径为2,则“蛋圆”的抛物线部分的解析式为分析:首先根据题意确定出A、B、D点的坐标.假设抛物线的解析式为y=ax2+bx+c.从图中可看到抛物线y=ax2+bx+c经过点A、B、D,联立组成方程组
,解得a、b、c的值,抛物线解析式即可确定.
首先根据M、半径确定出“蛋圆”半圆部分的解析式.再求得C点的坐标,根据C、M点坐标确定出直线CM的斜率,进而根据两直线垂直,斜率之积是-1.求得经过点C的“蛋圆”的切线的斜率,进而确定出切线的解析式.
|
首先根据M、半径确定出“蛋圆”半圆部分的解析式.再求得C点的坐标,根据C、M点坐标确定出直线CM的斜率,进而根据两直线垂直,斜率之积是-1.求得经过点C的“蛋圆”的切线的斜率,进而确定出切线的解析式.
解答:解:由题意得A(-1,0)、B(3,0)、D(0,-3)
∵抛物线y=ax2+bx+c经过点A、B、D
∴可列出方程组
,
解得c=-3、a=1、b=-2,
该抛物线的解析式为y=x2-2x-3.
∵半圆的圆心M(1,0),半径为2,
∴圆的解析式为半圆的解析式为(x-1)2+y2=4 (y≥0),
设点C的坐标为(0,k),
∵点C在半圆上,
∴1+k2=4,解得k=
即C点的坐标为(0,
),
则直线CM的解析式斜率为-
,
因而过点C圆M切线的解析式斜率为
=
故经过点C的“蛋圆”的切线的解析式为y-
=
(x-0),
即y=
x+
.
∵抛物线y=ax2+bx+c经过点A、B、D
∴可列出方程组
|
解得c=-3、a=1、b=-2,
该抛物线的解析式为y=x2-2x-3.
∵半圆的圆心M(1,0),半径为2,
∴圆的解析式为半圆的解析式为(x-1)2+y2=4 (y≥0),
设点C的坐标为(0,k),
∵点C在半圆上,
∴1+k2=4,解得k=
| 3 |
即C点的坐标为(0,
| 3 |
则直线CM的解析式斜率为-
| 3 |
因而过点C圆M切线的解析式斜率为
| -1 | ||
-
|
| ||
| 3 |
故经过点C的“蛋圆”的切线的解析式为y-
| 3 |
| ||
| 3 |
即y=
| ||
| 3 |
| 3 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有利用待定系数法求抛物线的解析式、直线解析式的确定、圆的切线问题.

练习册系列答案
相关题目
 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.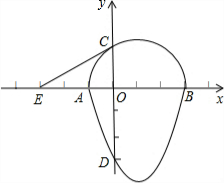 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2,则经过点C的“蛋圆”切线EC的解析式是
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2,则经过点C的“蛋圆”切线EC的解析式是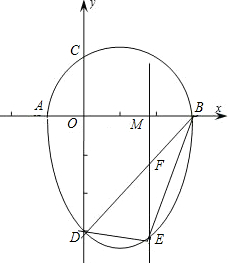 正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.
正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标. 仔细阅读并完成下题:
仔细阅读并完成下题: