题目内容
在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,要证明△ABC≌△A′B′C′,须添加一个条件,这个条件可以是①∠A=∠A′、②∠B=∠B′、③BC=B′C′中的
- A.①或②或③
- B.①或②
- C.①或③
- D.②或③
C
分析:根据全等三角形的判定定理SAS、SSS即可判断①②;根据全等三角形的判定定理SSS判断③即可.
解答: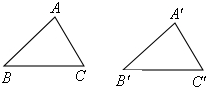 解:
解:
①∵AB=A′B′,∠A=∠A′,AC=A′C′,
∴△ABC≌△A′B′C′(SAS),∴①正确;
②根据SSA不能判断△ABC≌△A′B′C′,∴②错误;
③∵AB=A′B′,AC=A′C′,BC=B′C′,
∴△ABC≌△A′B′C′(SSS),∴③正确.
故选C.
点评:本题主要考查对全等三角形的判定的理解和掌握,能熟练地根据全等三角形的判定定理进行推理是解此题的关键.
分析:根据全等三角形的判定定理SAS、SSS即可判断①②;根据全等三角形的判定定理SSS判断③即可.
解答:
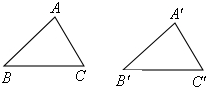 解:
解:①∵AB=A′B′,∠A=∠A′,AC=A′C′,
∴△ABC≌△A′B′C′(SAS),∴①正确;
②根据SSA不能判断△ABC≌△A′B′C′,∴②错误;
③∵AB=A′B′,AC=A′C′,BC=B′C′,
∴△ABC≌△A′B′C′(SSS),∴③正确.
故选C.
点评:本题主要考查对全等三角形的判定的理解和掌握,能熟练地根据全等三角形的判定定理进行推理是解此题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
 17、如图,在△ABC和△DEF中,AB=DE,当
17、如图,在△ABC和△DEF中,AB=DE,当 16、完成下面的证明过程:
16、完成下面的证明过程: 29、如图,在△ABC和△ADE中,AB=AD,AC=AE,∠DAC=∠BAE.
29、如图,在△ABC和△ADE中,AB=AD,AC=AE,∠DAC=∠BAE. 根据题意,把下列推理所依据的命题写出来,并指出是公理还是定理.
根据题意,把下列推理所依据的命题写出来,并指出是公理还是定理.