Question

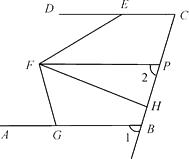
【题目】如图，在△ABC中，点D在边AC上，DB＝BC=AD，E是CD的中点，F是AB的中点，

(1)求证：EF＝AB.

(2) 当∠C=60 时， BC 、AB 与AC满足怎么样的关系？（直接写出答案，不必说明理由）

Answer 1

【答案】（1）证明见解析；（2）BC2+AB2=AC2.

【解析】试题分析：（1）连接BE，根据等腰三角形三线合一的性质可得BE⊥AC，再根据直角三角形斜边上的中线等于斜边的一半证明；（2）根据题意得出△BCD是等边三角形，得∠CBD=∠CDB=60°，再根据BD=AD，得出∠A=∠DBA=30°，再得出△ABC是直角三角形，从而得证.

解： (1)证明：连接BE,

∵BC=BD，E是CD的中点，

∴BE⊥AC，

又∵F是AB的中点，

∴EF＝AB.

(2)∵BC=BD，∠C=60 ，

∴△BCD是等边三角形，

∴∠CBD=∠CDB=60°，

∵BD=AD，

∴∠A=∠DBA=∠CDB=30°，

∴∠ABC=∠CBD+∠DBA=60°+30°=90°，

∴BC2+AB2=AC2.