题目内容
【题目】如图,四边形OABC是边长为4的正方形,点P从点O沿边OA向点A运动,每秒运动1个单位.连结CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点E作EF∥OA,交OB于点F,连结FD、BE,设点P运动的时间为![]()
![]() .
.
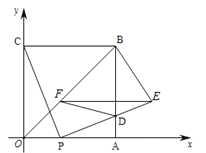
(1)点E的坐标为 (用含![]() 的代数式表示);
的代数式表示);
(2)试判断线段EF的长度是否随点P的运动变化而改变?并说明理由;
(3)当![]() 为何值时,四边形BEDF的面积为
为何值时,四边形BEDF的面积为![]() .
.
【答案】(1)、(4+t,t);(2)、不变,理由见解析;(3)、t=1或3.
【解析】
试题分析:(1)、过点E作EH⊥OA,垂足为H,从而得出点E的坐标;(2)、根据题意得出OA=OB=4,然后得出点F的坐标,根据点的坐标得出EF的长度;(3)、根据△DAP∽△POC得出BD的长度,然后根据四边形的面积列出方程得出答案.
试题解析:(1)、过点E作EH⊥OA,垂足为H. 点E的坐标为(4+![]() ,
,![]() ).
).
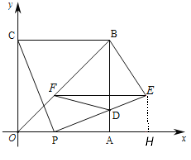
(2)、线段EF的长度不变.理由如下:
由题意知:OA=OB=4,∴点B坐标为(4,4),∠BOA=45°
∵EF∥OA,点E为(4+![]() ,
,![]() ),点F的坐标为(
),点F的坐标为(![]() ,
,![]() ) ∴EF=
) ∴EF=![]() =4,即线段EF的长度不变.
=4,即线段EF的长度不变.
(3)、由(1)知:∠DPA=∠PCO,又∠DAP=∠POC=90°
∴△DAP∽△POC,∴![]() ,∵OP=
,∵OP=![]() ,OC=4,∴AP=4-
,OC=4,∴AP=4-![]()
∴![]() ,∴AD=
,∴AD=![]() ,∴BD=
,∴BD=![]() =
=![]() ∵EF∥OA,AB⊥OA;∴EF⊥BD
∵EF∥OA,AB⊥OA;∴EF⊥BD
∵S四边形BEDF=![]() =
=![]() =
=![]()
解得t=1或t=3.所以,当![]() 为1、3时,四边形BEDF的面积为
为1、3时,四边形BEDF的面积为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目