题目内容
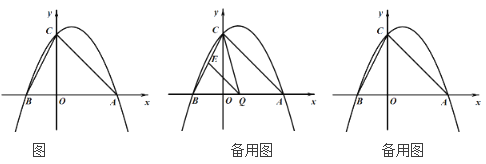
【题目】在平面直角坐标系xOy中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作d(M).
(1)已知点E(0,4),
①直接写出d(点E)的值;
②直线y=kx+4(k≠0)与x轴交于点F,当d(线段EF)取最小值时,求k的取值范围;
(2)⊙T的圆心为T(7,t),半径为1.若d(⊙T)<11,请直接写出t的取值范围.
【答案】(1)![]() ;(2)k≤-1或k≥1;(3)
;(2)k≤-1或k≥1;(3)![]() .
.
【解析】
(1)①由题意得点E到正方形ABCD边上C点间的距离最大值,EC=5,即d(点E)的值为5;
②由d(点E)=5得出d(线段EF)的最小值是5,得出符合题意的点F满足d(点F)≤5,求出当d(点F)=5时,BF1=DF2=5,得出点F1的坐标为(4,0),点F2的坐标为(-4,0),代入y=kx+4求出k的值,再结合函数图象即可得出结果;
(2)⊙T的圆心为T(7,t),半径为1,当d(⊙T)=11时,BM=BN=11,OH=7,得出T1B=T2B=10,BH=OB+OH=1+7=8,由勾股定理求出T1H和T2H,即可得出结果.
解:(1)①∵正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0),点E(0,4)在y轴上,
∴点E到正方形ABCD边上C点间的距离最大值,EC=5,
即d(点E)的值为5;
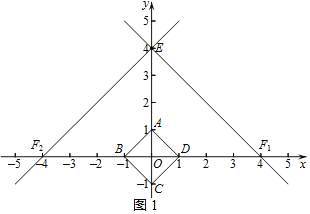
②如图1所示:∵d(点E)=5,
∴d(线段EF)的最小值是5,
∴符合题意的点F满足d(点F)≤5,
当d(点F)=5时,BF1=DF2=5,
∴点F1的坐标为(4,0),点F2的坐标为(-4,0),
将点F1的坐标代入y=kx+4得:0=4k+4,
解得:k=-1,
将点F2的坐标代入y=kx+4得:0=-4k+4,
解得:k=1,
∴k=-1或k=1.
∴当d(线段EF)取最小值时,EF1直线y=kx+4中k≤-1,EF2直线y=kx+4中k≥1,
∴当d(线段EF)取最小值时,k的取值范围为:k≤-1或k≥1;
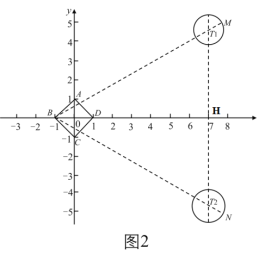
(2)⊙T的圆心为T(7,t),半径为1,
当d(⊙T)=11时,如图2所示:
BM=BN=11,OH=7,
∴T1B=T2B=10,BH=OB+OH=1+7=8,
∴T1H=![]() ,T2H=
,T2H=![]() ,
,
∴t的取值范围为:-6<t<6.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案