题目内容
(2012•绍兴)如图,直角三角形纸片ABC中,AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交于点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;…;设Pn-1Dn-2的中点为Dn-1,第n次将纸片折叠,使点A与点Dn-1重合,折痕与AD交于点Pn(n>2),则AP6的长为( )
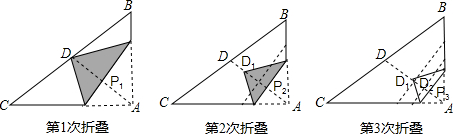

分析:先写出AD、AD1、AD2、AD3的长度,然后可发现规律推出ADn的表达式,继而根据APn=
ADn即可得出APn的表达式,也可得出AP6的长.
| 2 |
| 3 |
解答:解:由题意得,AD=
BC=
,AD1=AD-DD1=
,AD2=
,AD3=
,…,ADn=
,
又APn=
ADn,
故AP1=
,AP2=
,AP3=
…APn=
,
故可得AP6=
.
故选A.
| 1 |
| 2 |
| 5 |
| 2 |
| 5×31 |
| 23 |
| 5×32 |
| 25 |
| 5×33 |
| 27 |
| 5×3n |
| 22n+1 |
又APn=
| 2 |
| 3 |
故AP1=
| 5 |
| 4 |
| 15 |
| 16 |
| 5×32 |
| 26 |
| 5×3n-1 |
| 22n |
故可得AP6=
| 5×35 |
| 212 |
故选A.
点评:此题考查了翻折变换的知识,解答本题关键是写出前面几个有关线段长度的表达式,从而得出一般规律,注意培养自己的归纳总结能力.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
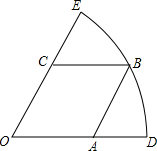 (2012•绍兴)如图,扇形DOE的半径为3,边长为
(2012•绍兴)如图,扇形DOE的半径为3,边长为
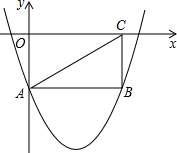 (2012•绍兴)如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(2012•绍兴)如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.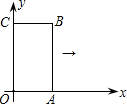 (2012•绍兴)如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为
(2012•绍兴)如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为