题目内容
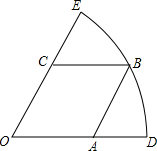 (2012•绍兴)如图,扇形DOE的半径为3,边长为
(2012•绍兴)如图,扇形DOE的半径为3,边长为| 3 |
 |
| DE |
分析:首先利用菱形的性质以及利用三角函数关系得出∠FOC=30°,进而得出底面圆锥的周长,即可得出底面圆的半径和母线长,利用勾股定理得出即可.
解答: 解:连接OB,AC,BO与AC相交于点F,
解:连接OB,AC,BO与AC相交于点F,
∵在菱形OABC中,AC⊥BO,CF=AF,FO=BF,∠COB=∠BOA,
又∵扇形DOE的半径为3,边长为
,
∴FO=BF=1.5,
cos∠FOC=
=
=
,
∴∠FOC=30°,
∴∠EOD=2×30°=60°,
∴
=
=π,
底面圆的周长为:2πr=π,
解得:r=
,圆锥母线为:3,
则此圆锥的高为:
=
,
故选:D.
 解:连接OB,AC,BO与AC相交于点F,
解:连接OB,AC,BO与AC相交于点F,∵在菱形OABC中,AC⊥BO,CF=AF,FO=BF,∠COB=∠BOA,
又∵扇形DOE的半径为3,边长为
| 3 |
∴FO=BF=1.5,
cos∠FOC=
| FO |
| CO |
| 1.5 | ||
|
| ||
| 2 |
∴∠FOC=30°,
∴∠EOD=2×30°=60°,
∴
 |
| DE |
| 60π×3 |
| 180 |
底面圆的周长为:2πr=π,
解得:r=
| 1 |
| 2 |
则此圆锥的高为:
32-
|
| ||
| 2 |
故选:D.
点评:此题主要考查了菱形的性质以及圆锥与侧面展开图的对应关系,根据圆锥的底面圆的周长等于扇形弧长是解题关键.

练习册系列答案
相关题目
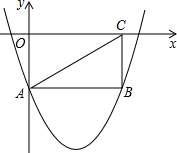 (2012•绍兴)如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(2012•绍兴)如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.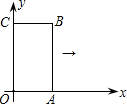 (2012•绍兴)如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为
(2012•绍兴)如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为