题目内容
在Rt△ABC中,∠ACB=90°,AC=6,BC=8,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.设点D运动的时间为t秒.
(1)如图1,过点D作DH⊥AB于H,当t为何值时,△ADH≌△ABC,并求出此时DE的长度;
(2)如图2,过点B作射线BP∥AC,过点E作EF⊥AC交射线BP于F,G是EF中点,连接DG.当△DEG与△ACB相似时,求t的值.

解:(1)∵在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴BA= =
=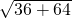 =10,
=10,
∵当△ADH≌△ABC时,AB=AD,AC=AH,
∵动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,
∴5t=10,即t=2;
AE=AC+CE=6+3t=6+6=12,DE=AE-AD=12-10=2;
(2)∵EF=BC=8,G是EF的中点,
∴GE=4.
当AD<AE(即t<3)时,DE=AE-AD=6+3t-5t=6-2t,
若△DEG与△ACB相似,则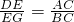 或
或 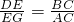 ,
,
∴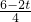 =
=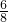 或
或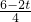 =
= ,
,
∴t= 或t=
或t= ,
,
当AD>AE(即t>3)时,DE=AD-AE=5t-(6+3t)=2t-6,
若△DEG与△ACB相似,则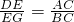 或
或 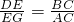 ,
,
∴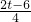 =
=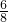 或
或 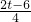 =
= ,
,
解得t= 或t=
或t= .
.
综上所述,当t= 或
或 或
或 或
或 时,△DEG与△ACB相似.
时,△DEG与△ACB相似.
分析:(1)在Rt△ABC中,利用勾股定理可求得AB的长,即可得到AD、t的值,从而确定AE的长,由DE=AE-AD即可得解.
(2)若△DEG与△ACB相似,要分两种情况:①AG:DE=DH:GE,②AH:EG=DH:DE,根据这些比例线段即可求得t的值.(需注意的是在求DE的表达式时,要分AD>AE和AD<AE两种情况)
点评:此题考查了勾股定理、全等三角形判定和性质、相似三角形等相关知识,综合性强,是一道难度较大的压轴题.
∴BA=
 =
=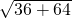 =10,
=10,∵当△ADH≌△ABC时,AB=AD,AC=AH,
∵动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,
∴5t=10,即t=2;
AE=AC+CE=6+3t=6+6=12,DE=AE-AD=12-10=2;
(2)∵EF=BC=8,G是EF的中点,
∴GE=4.
当AD<AE(即t<3)时,DE=AE-AD=6+3t-5t=6-2t,
若△DEG与△ACB相似,则
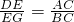 或
或 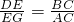 ,
,∴
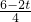 =
=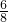 或
或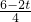 =
= ,
,∴t=
 或t=
或t= ,
,当AD>AE(即t>3)时,DE=AD-AE=5t-(6+3t)=2t-6,
若△DEG与△ACB相似,则
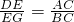 或
或 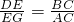 ,
,∴
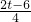 =
=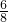 或
或 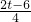 =
= ,
,解得t=
 或t=
或t= .
.综上所述,当t=
 或
或 或
或 或
或 时,△DEG与△ACB相似.
时,△DEG与△ACB相似.分析:(1)在Rt△ABC中,利用勾股定理可求得AB的长,即可得到AD、t的值,从而确定AE的长,由DE=AE-AD即可得解.
(2)若△DEG与△ACB相似,要分两种情况:①AG:DE=DH:GE,②AH:EG=DH:DE,根据这些比例线段即可求得t的值.(需注意的是在求DE的表达式时,要分AD>AE和AD<AE两种情况)
点评:此题考查了勾股定理、全等三角形判定和性质、相似三角形等相关知识,综合性强,是一道难度较大的压轴题.

练习册系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )