题目内容
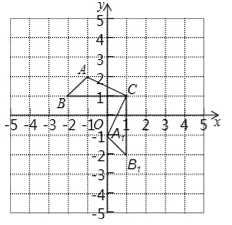
【题目】如图，函数y=﹣2x+3与y=﹣ 
x+m的图象交于P（n，﹣2）．
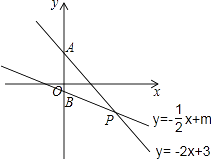
（1）求出m、n的值；
（2）求出△ABP的面积．
【答案】
（1）解：∵y=﹣2x+3与y=﹣ 
x+m的图象交于P（n，﹣2）．
∴﹣2=﹣2n+3，
∴n= 
，
∴P（ ，﹣2），
∴﹣2=﹣ × +m，
∴m=﹣ 
；
（2）解：∵在y=﹣2x+3中，令x=0，得y=3，
∴A（0，3），
∵在y=﹣ x﹣ 中，令x=0，得y=﹣ ，
∴B（0，﹣ ），
∴AB= 
，
∴△ABP的面积= 
× = 
．
【解析】（1）先把P（n，-2）代入y=-2x+3即可得到n的值，从而得到P点坐标为（,-2），然后把P点坐标代入y=-x+m可计算出m的值；
（2）解方程确定A，B点坐标，然后根据三角形面积公式求解.
高中必刷题系列答案
【题目】某超市经销A、B两种商品，A种商品每件进价20元，售价30元；B种商品每件进价35元，售价48元．
（1）该超市准备用800元去购进A、B两种商品若干件，怎样购进才能使超市经销这两种商品所获利润最大？（其中B种商品不少于7件）
（2）在“五一”期间，该商场对A、B两种商品进行如下优惠促销活动：
打折前一次购物总金额 | 优惠措施 |
不超过300元 | 不优惠 |
超过300元且不超过400元 | 售价打八折 |
超过400元 | 售价打七折 |
促销活动期间小颖去该超市购买A种商品，小华去该超市购买B种商品，分别付款210元与268.8元．促销活动期间小明决定一次去购买小颖和小华购买的同样多的商品，他需付款多少元？
【题目】某校举办八年级学生数学素养大赛，比赛共设四个项目：七巧板拼图，趣题巧解，数学应用，魔方复原，每个项目得分都按一定百分比折算后记入总分，下表为甲，乙，丙三位同学得分情况（单位：分）
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
（1）比赛后，甲猜测七巧板拼图，趣题巧解，数学应用，魔方复原这四个项目得分分别按10%，40%，20%，30%折算记入总分，根据猜测，求出甲的总分；
（2）本次大赛组委会最后决定，总分为80分以上（包含80分）的学生获一等奖，现获悉乙，丙的总分分别是70分，80分．甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分，问甲能否获得这次比赛的一等奖？