题目内容
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为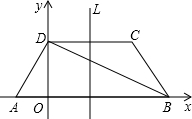 x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.
x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其对称轴L;
(3)若P是抛物线的对称轴L上的点,那么使△PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
解:(1)∵DC∥AB,AD=DC=CB,
∴∠CDB=∠CBD=∠DBA
∠DAB=∠CBA,
∴∠DAB=2∠DBA,(1分
∠DAB+∠DBA=90°,
∴∠DAB=60°
∠DBA=30°,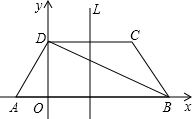
∵AB=4,
∴DC=AD=2,
Rt△AOD,OA=1,OD= ,AD=2.
,AD=2.
∴A(-1,0),D(0, ),C(2,
),C(2, ).
).
(2)根据抛物线和等腰梯形的对称性知,满足条件的抛物线必过点A(-1,0),B(3,0),
故可设所求为y=a(x+1)(x-3)
将点D(0, )的坐标代入上式得,a=
)的坐标代入上式得,a= .
.
所求抛物线的解析式为y=- (x+1)(x-3),
(x+1)(x-3),
其对称轴L为直线x=1.
(3)△PDB为等腰三角形,有以下三种情况:
①因直线L与DB不平行,DB的垂直平分线与L仅有一个交点P1,P1D=P1B,
△P1DB为等腰三角形;
②因为以D为圆心,DB为半径的圆与直线L有两个交点P2、P3,DB=DP2,DB=DP3,△P2DB,△P3DB为等腰三角形;
③与②同理,L上也有两个点P4、P5,使得BD=BP4,BD=BP5.
由于以上各点互不重合,所以在直线L上,使△PDB为等腰三角形的点P有5个.
分析:(1)已知AD=DC=CB,根据等边对等角,以及平行线的性质.可以得到,∠CDB=∠CBD=∠DBA.若设,∠CDB=∠CBD=∠DBA=x度,则∠ABC=2x度,∠C=90+x度.根据平行线的性质同旁内角互补,就可以求出x的值.在直角△ABD和直角△AOD中,根据三角函数,就可以求出OA、OD的长度,就可以得到A,D,C的坐标.
(2)已知A,D,C的坐标,根据待定系数法就可以求出抛物线的解析式以及对称轴.
(3)△PDB为等腰三角形,应分BD是底边,和BD是腰两种情况进行讨论.而BD是腰又要分D是顶角的顶点和B是顶角的顶点两种情况进行讨论.
点评:本题主要考查了梯形的有关计算,以及待定系数法求函数的解析式,正确地进行讨论是解决本题的关键.
∴∠CDB=∠CBD=∠DBA
∠DAB=∠CBA,
∴∠DAB=2∠DBA,(1分
∠DAB+∠DBA=90°,
∴∠DAB=60°
∠DBA=30°,

∵AB=4,
∴DC=AD=2,
Rt△AOD,OA=1,OD=
 ,AD=2.
,AD=2.∴A(-1,0),D(0,
 ),C(2,
),C(2, ).
).(2)根据抛物线和等腰梯形的对称性知,满足条件的抛物线必过点A(-1,0),B(3,0),
故可设所求为y=a(x+1)(x-3)
将点D(0,
 )的坐标代入上式得,a=
)的坐标代入上式得,a= .
.所求抛物线的解析式为y=-
 (x+1)(x-3),
(x+1)(x-3),其对称轴L为直线x=1.
(3)△PDB为等腰三角形,有以下三种情况:
①因直线L与DB不平行,DB的垂直平分线与L仅有一个交点P1,P1D=P1B,
△P1DB为等腰三角形;
②因为以D为圆心,DB为半径的圆与直线L有两个交点P2、P3,DB=DP2,DB=DP3,△P2DB,△P3DB为等腰三角形;
③与②同理,L上也有两个点P4、P5,使得BD=BP4,BD=BP5.
由于以上各点互不重合,所以在直线L上,使△PDB为等腰三角形的点P有5个.
分析:(1)已知AD=DC=CB,根据等边对等角,以及平行线的性质.可以得到,∠CDB=∠CBD=∠DBA.若设,∠CDB=∠CBD=∠DBA=x度,则∠ABC=2x度,∠C=90+x度.根据平行线的性质同旁内角互补,就可以求出x的值.在直角△ABD和直角△AOD中,根据三角函数,就可以求出OA、OD的长度,就可以得到A,D,C的坐标.
(2)已知A,D,C的坐标,根据待定系数法就可以求出抛物线的解析式以及对称轴.
(3)△PDB为等腰三角形,应分BD是底边,和BD是腰两种情况进行讨论.而BD是腰又要分D是顶角的顶点和B是顶角的顶点两种情况进行讨论.
点评:本题主要考查了梯形的有关计算,以及待定系数法求函数的解析式,正确地进行讨论是解决本题的关键.

练习册系列答案
相关题目
 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.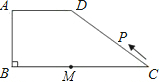 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有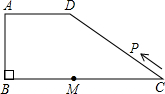 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.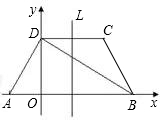 如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是 如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )
如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )