题目内容
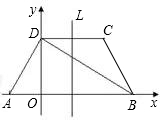 如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是分析:首先根据等腰梯形的性质,可证得BD是∠CBA的平分线,即可求得∠ABD的度数,则可求得AD的长;求交点,可以从PB=PD,PD=BD,PB=BD三种情况分析,注意结合图形求解较简单.
解答:解:∵AB∥CD,
∴∠DBA=∠CDB,
∵DC=CB,
∴∠CDB=∠CBD,
∴∠CBD=∠DBA,
∵AD=BC,
∴∠A=∠ABC=2∠ABD,
∵AD⊥DB,
∴∠ADB=90°,
∴∠ABD=30°,
∴AD=
AB=2;
∵若△PDB为等腰三角形,
若PD=PB,则点P是BD的垂直平分线与L的交点,有一个;
若PD=BD,则点P是以点D为圆心,BD的长为半径作圆与直线L的交点,有两个;
若PB=BD,则点P是以点B为圆心,BD的长为半径作圆与直线L的交点,有两个;
所以共有5个.
∴∠DBA=∠CDB,
∵DC=CB,
∴∠CDB=∠CBD,
∴∠CBD=∠DBA,
∵AD=BC,
∴∠A=∠ABC=2∠ABD,
∵AD⊥DB,
∴∠ADB=90°,
∴∠ABD=30°,
∴AD=
| 1 |
| 2 |
∵若△PDB为等腰三角形,
若PD=PB,则点P是BD的垂直平分线与L的交点,有一个;
若PD=BD,则点P是以点D为圆心,BD的长为半径作圆与直线L的交点,有两个;
若PB=BD,则点P是以点B为圆心,BD的长为半径作圆与直线L的交点,有两个;
所以共有5个.
点评:此题考查了等腰梯形的性质、等腰三角形的性质以及直角三角形的性质.解题时注意数形结合思想的应用.注意求点P时要用分类讨论的思想求解.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
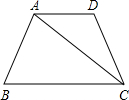 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.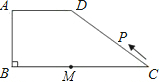 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有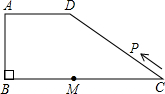 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长. 如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )
如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( )