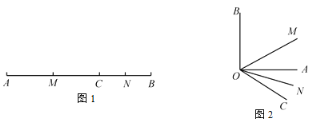题目内容
【题目】阅读:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为![]() ,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
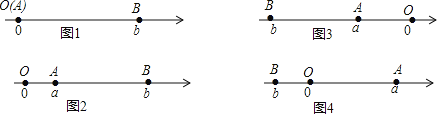
当A、B两点都不在原点时,如图2,点A、B都在原点的右边∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;如图3,点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;如图4,点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= a +(-b)=∣a-b∣;
回答下列问题:
(1)数轴上表示3和5的两点之间的距离是_________,数轴上表示-3和-5的两点之间的距离是_________,数轴上表示1和-2的两点之间的距离是 ;
(2)数轴上表示x和-1的两点A和B之间的距离是 ,如果∣AB∣=3,那么x为 ;
(3)当代数式∣x+3∣+∣x-2∣取最小值时,相应的x的取值范围是 ;当![]() 为 时,该代数式为7.
为 时,该代数式为7.
【答案】(1)2,2,3;(2)![]() ,2或-4;(3)
,2或-4;(3)![]() ,-4或3.
,-4或3.
【解析】
(1)(2)根据数轴上A、B两点之间的距离![]() ,代入数值即可求出;
,代入数值即可求出;
(3)代数式![]() 的最小值,意思是数轴上数x到-3的距离与到2 的距离之和最小,据此即可求出x的范围;若
的最小值,意思是数轴上数x到-3的距离与到2 的距离之和最小,据此即可求出x的范围;若![]() ,在中间的时候代数式的值是5,只要在-3的左侧和2的右侧各找到一个到最近点距离为1的点就是所求.
,在中间的时候代数式的值是5,只要在-3的左侧和2的右侧各找到一个到最近点距离为1的点就是所求.
解:(1)数轴上表示3和5的两点之间的距离是![]() ;
;
数轴上表示-3和-5的两点之间的距离是![]() ;
;
数轴上表示1和-2的两点之间的距离是![]() ;
;
(2)数轴上表示x和-1的两点A和B之间的距离是![]() ;
;
如果![]() ,则
,则![]() ,所以
,所以![]() 或
或![]() ,解得:x=2或-4;
,解得:x=2或-4;
(3)代数式![]() 的最小值,意思是数轴上数x到-3的距离与到2 的距离之和最小,那么x应在-3与2之间的线段上,所以
的最小值,意思是数轴上数x到-3的距离与到2 的距离之和最小,那么x应在-3与2之间的线段上,所以![]() ,这个最小值是
,这个最小值是![]() ;
;
若![]() ,在
,在![]() 时,
时,![]() =5,所以只要在数轴上-3的左侧和2的右侧各找到一个到-3的距离和到2的距离为1的点就是所求,在数轴上-3的左侧的数是-4,2的右侧的数是3,所以当x=-4或3时,
=5,所以只要在数轴上-3的左侧和2的右侧各找到一个到-3的距离和到2的距离为1的点就是所求,在数轴上-3的左侧的数是-4,2的右侧的数是3,所以当x=-4或3时,![]() .
.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
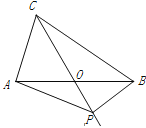
成功训练计划系列答案【题目】在数轴上![]() 、
、![]() 两点分别表示有理数
两点分别表示有理数![]() 和
和![]() ,我们用
,我们用![]() 表示
表示![]() 到
到![]() 之间的距离;例如
之间的距离;例如![]() 表示7到3之间的距离.
表示7到3之间的距离.
(1)当![]() 时,
时,![]() 的值为 .
的值为 .
(2)如何理解![]() 表示的含义?
表示的含义?
(3)若点![]() 、
、![]() 在0到3(含0和3)之间运动,求
在0到3(含0和3)之间运动,求![]() 的最小值和最大值.
的最小值和最大值.
【题目】骑共享单车已成为人们喜爱的一种绿色出行方式.已知A、B、C三家公司的共享单车都是按骑车时间收费,标准如下:
公司 | 单价(元/半小时) | 充值优惠 |
A | m | 充20元送5元,即:充20元实得25元 |
B | m-0.2 | 无 |
C | 1 | 充20元送20元,即:充20元实得40元 |
(注:使用这三家公司的共享单车,不足半小时均按半小时计费.用户的账户余额长期有效,但不可提现.)
4月初,李明注册成了A公司的用户,张红注册成了B公司的用户,并且两人在各自账户上分别充值20元.一个月下来,李明、张红两人使用单车的次数恰好相同,且每次都在半小时以内,结果到月底李明、张红的账户余额分别显示为5元、8元.
(1)求m的值;
(2)5月份,C公司在原标准的基础上又推出新优惠:每月的月初给用户送出5张免费使用券(1
次用车只能使用1张券).如果王磊每月使用单车的次数相同,且在30次以内,每次用车都不超过
半小时. 若要在这三家公司中选择一家并充值20元,仅从资费角度考虑,请你帮他作出选择,并说
明理由.
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?