题目内容
在等腰梯形ABCD中,AD∥BC,AD=3,AB=CD=4,BC=5,∠B的平分线交DC于点E,交AD的延长线于点F.(1)如图(1),若∠C的平分线交BE于点G,写出图中所有的相似三角形(不必证明);
(2)在(1)的条件下求BG的长;
(3)若点P为BE上动点,以点P为圆心,BP为半径的⊙P与线段BC交于点Q(如图(2)),请直接写出当BP取什么范围内值时,①点A在⊙P内;②点A在⊙P内而点E在⊙P外.
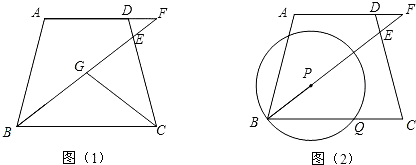
分析:(1)利用平行线的性质和角平分线定义找到相等的角,进一步根据两角对应相等证明三角形相似;
(2)根据平行线的性质和角平分线定义,得∠ABE=∠AFB,则AB=AF=4,则DF=1;根据平行线分线段成比例定理求得DE和CE的长;根据等腰梯形的性质和角平分线定义,得BG=CG;设BG=CG=x,根据△FDE∽△CGE,求得BG的长;
(3)根据点和圆的位置关系与数量之间的联系进行分析.
(2)根据平行线的性质和角平分线定义,得∠ABE=∠AFB,则AB=AF=4,则DF=1;根据平行线分线段成比例定理求得DE和CE的长;根据等腰梯形的性质和角平分线定义,得BG=CG;设BG=CG=x,根据△FDE∽△CGE,求得BG的长;
(3)根据点和圆的位置关系与数量之间的联系进行分析.
解答:解:(1)△ABF∽△GBC,△FDE∽△CGE∽△BCE.
(2)∵BE平分∠B,
∴∠ABE=∠EBC,
∵AD∥BC,
∴∠AFB=∠EBC,
∴∠ABE=∠AFB,
∴AB=AF.
∴AF=4,DF=1.
∵AD∥BC,
∴DF:BC=DE:EC,
∴DE=
,CE=
.
∵AD∥BC,AB=CD,
∴∠BCD=∠ABC.
∵CG平分∠BCD,BE平分∠ABC,
∴∠CBG=∠BCG,
∴BG=CG.
设BG=CG=x,则由△FDE∽△CGE,得
DF:CG=DE:GE,
∴GE=
x.
又由△CGE∽△BCE,得
EC2=EG•EB,
即(
)2=
x•(x+
x),
∴x=
,
即BG=
.
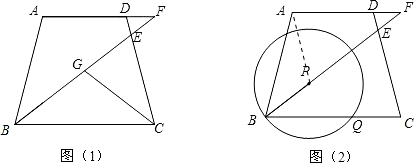
(3)①连接AP,当BP=AP时,点A在圆P上,此时△ABP∽△ABF,求得BP=
,
即BP>AP时,点A在⊙P内.
∴当
<BP≤
时,点A在⊙P内.
②根据①求得BE=
,
∴BP<
BE,即BP<
时,点A在⊙P内而点E在⊙P外
∴当
<BP<
时,点A在⊙P内而点E在⊙P外.
(2)∵BE平分∠B,
∴∠ABE=∠EBC,
∵AD∥BC,
∴∠AFB=∠EBC,
∴∠ABE=∠AFB,
∴AB=AF.
∴AF=4,DF=1.
∵AD∥BC,
∴DF:BC=DE:EC,
∴DE=
| 2 |
| 3 |
| 10 |
| 3 |
∵AD∥BC,AB=CD,
∴∠BCD=∠ABC.
∵CG平分∠BCD,BE平分∠ABC,
∴∠CBG=∠BCG,
∴BG=CG.
设BG=CG=x,则由△FDE∽△CGE,得
DF:CG=DE:GE,
∴GE=
| 2 |
| 3 |
又由△CGE∽△BCE,得
EC2=EG•EB,
即(
| 10 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴x=
| 10 |
即BG=
| 10 |

(3)①连接AP,当BP=AP时,点A在圆P上,此时△ABP∽△ABF,求得BP=
| 4 |
| 5 |
| 10 |
即BP>AP时,点A在⊙P内.
∴当
| 4 |
| 5 |
| 10 |
| 10 |
②根据①求得BE=
| 5 |
| 3 |
| 10 |
∴BP<
| 1 |
| 2 |
| 5 |
| 6 |
| 10 |
∴当
| 4 |
| 5 |
| 10 |
| 5 |
| 6 |
| 10 |
点评:此题综合考查了相似三角形的判定和性质以及点和圆的位置关系与数量之间的联系.

练习册系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.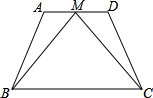 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.